
已知圆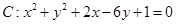 ,直线
,直线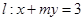 .
.
(Ⅰ)若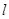 与
与 相切,求
相切,求 的值;
的值;
(Ⅱ)是否存在 值,使得
值,使得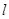 与
与 相交于
相交于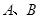 两点,且
两点,且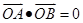 (其中
(其中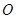 为坐标原点),若存在,求出
为坐标原点),若存在,求出 ,若不存在,请说明理由.
,若不存在,请说明理由.
(Ⅰ)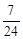 (Ⅱ)m=9±2
(Ⅱ)m=9±2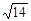
【解析】
试题分析:(Ⅰ)由圆方程配方得(x+1)2+(y-3)2=9,
圆心为C(-1,3),半径为 r = 3, 2分
若 l与C相切,则得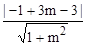 =3,
=3,
∴(3m-4)2=9(1+m2),∴m =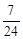 . 5分
. 5分
(Ⅱ)假设存在m满足题意。
由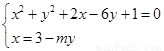 ,消去x得
,消去x得
(m2+1)y2-(8m+6)y+16=0,
由△=(8m+6)2-4(m2+1)·16>0,得m>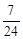 , 8分
, 8分
设A(x1,y1),B(x2,y2),则y1+y2=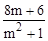 ,y1y2=
,y1y2=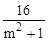 .
.

 OA·OB=x1x2+y1y2
OA·OB=x1x2+y1y2
=(3-my1)(3-my2)+y1y2
=9-3m(y1+y2)+(m2+1)y1y2
=9-3m·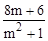 +(m2+1)·
+(m2+1)·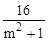
=25-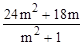 =0
10分
=0
10分
24m2+18m=25m2+25,m2-18m+25=0,
∴m=9±2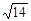 ,适合m>
,适合m>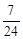 ,
,
∴存在m=9±2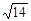 符合要求.
符合要求.
考点:直线与圆相切相交的位置关系
点评:直线与圆相切,一般用圆心到直线的距离等于圆的半径,本题直线与圆相交联立方程利用韦达定理可得到焦点坐标与方程的关系,进而可将向量坐标化化简


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2013-2014学年河北唐山市高三年级第一学期期末考试理科数学试卷(解析版) 题型:解答题
已知圆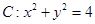 ,直线
,直线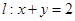 ,以O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系.
,以O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系.
(1)将圆C和直线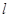 方程化为极坐标方程;
方程化为极坐标方程;
(2)P是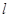 上的点,射线OP交圆C于点R,又点Q在OP上且满足
上的点,射线OP交圆C于点R,又点Q在OP上且满足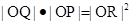 ,当点P在
,当点P在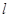 上移动时,求点Q轨迹的极坐标方程.
上移动时,求点Q轨迹的极坐标方程.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年辽宁省高三上学期期中考试理科数学试卷(解析版) 题型:选择题
已知圆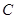 与直线
与直线 及
及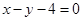 都相切,圆心在直线
都相切,圆心在直线 上,则圆
上,则圆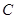 的方程为( )
的方程为( )
A、 B、
B、
C、 D、
D、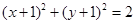
查看答案和解析>>
科目:高中数学 来源:2013届北京市高二上学期期中考试数学试卷 题型:解答题
已知圆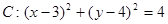 和直线
和直线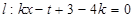 ,
,
(1)求证:不论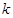 取什么值,直线和圆总相交;
取什么值,直线和圆总相交;
(2)求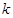 取何值时,直线被圆截得的弦最短,并求出最短弦的长;
取何值时,直线被圆截得的弦最短,并求出最短弦的长;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com