
ЁОЬтФПЁП2019Фъ10дТ20ШеЃЌЕкСљНьЪРНчЛЅСЊЭјДѓЛсЗЂВМСЫ15ЯюЁАЪРНчЛЅСЊЭјСьЯШПЦММГЩЙћЁБЃЌЦфжага5ЯюГЩЙћОљЪєгкаОЦЌСьгђЃЌЗжБ№ЮЊЛЊЮЊИпадФмЗўЮёЦїаОЦЌЁАіяХє920ЁБЁЂЧхЛЊДѓбЇЁАУцЯђЭЈгУШЫЙЄжЧФмЕФвьЙЙШкКЯЬьЛњаОЦЌЁБЁЂЁАЬиЫЙРШЋздЖЏМнЪЛаОЦЌЁБЁЂКЎЮфМЭдЦЖЫAIаОЦЌЁЂЁАЫМдЊ270ЁБЁЂШќСщЫМЁАVersalздЪЪгІМЦЫуМгЫйЦНЬЈЁБЃЎЯжга3УћбЇЩњДгет15ЯюЁАЪРНчЛЅСЊЭјСьЯШПЦММГЩЙћЁБжаЗжБ№ШЮбЁ1ЯюНјааСЫНтЃЌЧвбЇЩњжЎМфЕФбЁдёЛЅВЛгАЯьЃЌдђжСЩйга1УћбЇЩњбЁдёЁАаОЦЌСьгђЁБЕФИХТЪЮЊЃЈ ЃЉ
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ЁОД№АИЁПD
ЁОНтЮіЁП
ЯШМЦЫуГіУПУћбЇЩњбЁдёЁАаОЦЌСьгђЁБЕФИХТЪЮЊ![]() ,дйИљОнЖРСЂЪТМўЕФИХТЪМЦЫуЙЋЪНМЦЫуГі3УћбЇЩњОљУЛгабЁдёЁАаОЦЌСьгђЁБЕФИХТЪ,НјЖјЕУГіД№АИ.
,дйИљОнЖРСЂЪТМўЕФИХТЪМЦЫуЙЋЪНМЦЫуГі3УћбЇЩњОљУЛгабЁдёЁАаОЦЌСьгђЁБЕФИХТЪ,НјЖјЕУГіД№АИ.
ИљОнЬтвтПЩжЊ,1УћбЇЩњДг15ЯюжаШЮбЁ1Яю,ЦфбЁдёЁАаОЦЌСьгђЁБЕФИХТЪЮЊ![]() ,
,
ЙЪЦфУЛгабЁдёЁАаОЦЌСьгђЁБЕФИХТЪЮЊ![]() ,
,
дђ3УћбЇЩњОљУЛгабЁдёЁАаОЦЌСьгђЁБЕФИХТЪЮЊ![]() ,
,
вђДЫжСЩйга1УћбЇЩњбЁдёЁАаОЦЌСьгђЁБЕФИХТЪЮЊ![]() ,
,
ЙЪбЁ:D.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() .
.
ЃЈ1ЃЉжЄУїЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЃЈiЃЉжЄУїЃКЕБ![]() ЪБЃЌЖдШЮвт
ЪБЃЌЖдШЮвт![]() ЃЌзмга
ЃЌзмга![]() ЃЛ
ЃЛ
ЃЈiiЃЉЬжТлКЏЪ§![]() ЕФСуЕуИіЪ§.
ЕФСуЕуИіЪ§.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєКЏЪ§fЃЈxЃЉдкЦфЭМЯѓЩЯДцдкВЛЭЌЕФСНЕуAЃЈx1ЃЌy1ЃЉЃЌBЃЈx2ЃЌy2ЃЉЃЌЦфзјБъТњзуЬѕМўЃК|x1x2+y1y2|![]() ЕФзюДѓжЕЮЊ0ЃЌдђГЦfЃЈxЃЉЮЊЁАПТЮїКЏЪ§ЁБЃЌдђЯТСаКЏЪ§ЃК
ЕФзюДѓжЕЮЊ0ЃЌдђГЦfЃЈxЃЉЮЊЁАПТЮїКЏЪ§ЁБЃЌдђЯТСаКЏЪ§ЃК
ЂйfЃЈxЃЉЃНx![]() ЃЈxЃО0ЃЉЃЛ
ЃЈxЃО0ЃЉЃЛ
ЂкfЃЈxЃЉЃНlnxЃЈ0ЃМxЃМ3ЃЉЃЛ
ЂлfЃЈxЃЉЃНcosxЃЛ
ЂмfЃЈxЃЉЃНx2Љ1.
ЦфжаЮЊЁАПТЮїКЏЪ§ЁБЕФИіЪ§ЮЊЃЈ ЃЉ
A.1B.2C.3D.4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЭждВ![]() ЃК
ЃК![]() ЕФРыаФТЪЮЊ
ЕФРыаФТЪЮЊ![]() ЃЌАыНЙОрЮЊ
ЃЌАыНЙОрЮЊ![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() жсЁЂ
жсЁЂ![]() жсЕФДЙЯпЃЌДЙзуЗжБ№Еу
жсЕФДЙЯпЃЌДЙзуЗжБ№Еу![]() ЃЌ
ЃЌ![]() ЃЌЧвЫФБпаЮ
ЃЌЧвЫФБпаЮ![]() ЕФУцЛ§ЮЊ2.
ЕФУцЛ§ЮЊ2.
ЃЈ1ЃЉЧѓЭждВ![]() ЕФБъзМЗНГЬЃЛ
ЕФБъзМЗНГЬЃЛ
ЃЈ2ЃЉвбжЊОЙ§Еу![]() ЕФжБЯп
ЕФжБЯп![]() гыЭждВ
гыЭждВ![]() НЛгк
НЛгк![]() ЃЌ
ЃЌ![]() СНЕуЃЌЩшжБЯп
СНЕуЃЌЩшжБЯп![]() гыжБЯп
гыжБЯп![]() ЕФЧуаБНЧЗжБ№ЮЊ
ЕФЧуаБНЧЗжБ№ЮЊ![]() ЃЌ
ЃЌ![]() ЃЌЧв
ЃЌЧв![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃДг2011ФъЕН2018ФъВЮМгЁАББдМЁБЁАЛЊдМЁБПМЪдЖјЛёЕУМгЗжЕФбЇЩњЃЈУПЮЛбЇЩњжЛФмВЮМгЁАББдМЁБЁАЛЊдМЁБжаЕФвЛжжПМЪдЃЉШЫЪ§ПЩвдЭЈЙ§вдЯТБэИёЗДгГГіРД.ЃЈЮЊСЫЗНБуМЦЫуЃЌНЋ2011ФъБрКХЮЊ1ЃЌ2012ФъБрКХЮЊ2ЃЌвРДЫРрЭЦЃЉ
ФъЗн | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
ШЫЪ§ | 2 | 3 | 4 | 4 | 7 | 7 | 6 | 6 |
ЃЈ1ЃЉЧѓетАЫФъРДЃЌИУаЃВЮМгЁАББдМЁБЁАЛЊдМЁБПМЪдЖјЛёЕУМгЗжЕФбЇЩњШЫЪ§ЕФжаЮЛЪ§КЭЗНВюЃЛ
ЃЈ2ЃЉИљОнзюНќЮхФъЕФЪ§ОнЃЌРћгУзюаЁЖўГЫЗЈЧѓГі![]() гы
гы![]() жЎМфЕФЯпадЛиЙщЗНГЬЃЌВЂвРДЫдЄВтИУаЃ2019ФъВЮМгЁАББдМЁБЁАЛЊдМЁБПМЪдЖјЛёЕУМгЗжЕФбЇЩњШЫЪ§.ЃЈНсЙћвЊЧѓЫФЩсЮхШыжСИіЮЛЃЉ
жЎМфЕФЯпадЛиЙщЗНГЬЃЌВЂвРДЫдЄВтИУаЃ2019ФъВЮМгЁАББдМЁБЁАЛЊдМЁБПМЪдЖјЛёЕУМгЗжЕФбЇЩњШЫЪ§.ЃЈНсЙћвЊЧѓЫФЩсЮхШыжСИіЮЛЃЉ
ВЮПМЙЋЪНЃК .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЬжТлКЏЪ§![]() ЕФЕЅЕїадЃЛ
ЕФЕЅЕїадЃЛ
ЃЈ2ЃЉЕБ![]() ЪБЃЌЧѓКЏЪ§
ЪБЃЌЧѓКЏЪ§![]() дк
дк![]() ЩЯЕФСуЕуИіЪ§ЃЎ
ЩЯЕФСуЕуИіЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯп![]() ЃЌЧвХзЮяЯп
ЃЌЧвХзЮяЯп![]() дкЕу
дкЕу![]() ДІЕФЧаЯпаБТЪЮЊ
ДІЕФЧаЯпаБТЪЮЊ![]() ЃЌжБЯп
ЃЌжБЯп![]() гыХзЮяЯпНЛгк
гыХзЮяЯпНЛгк![]() СНЕуЃЈЕу
СНЕуЃЈЕу![]() дкЕу
дкЕу![]() зѓВрЃЉЃЌЧвжБЯп
зѓВрЃЉЃЌЧвжБЯп![]() ДЙжБгкжБЯп
ДЙжБгкжБЯп![]() ЃЎ
ЃЎ
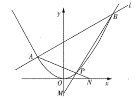
ЃЈ1ЃЉЧѓжЄЃКжБЯп![]() Й§ЖЈЕуЃЌВЂЧѓГіЖЈЕузјБъЃЛ
Й§ЖЈЕуЃЌВЂЧѓГіЖЈЕузјБъЃЛ
ЃЈ2ЃЉШчЭМЃЌжБЯп![]() НЛ
НЛ![]() жсгкЕу
жсгкЕу![]() ЃЌжБЯп
ЃЌжБЯп![]() НЛ
НЛ![]() жсгкЕуЃЌЧѓ
жсгкЕуЃЌЧѓ![]() ЕФзюДѓжЕЃЎ
ЕФзюДѓжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПбЁао4ЁЊ4ЃКзјБъЯЕгыВЮЪ§ЗНГЬЁЃ
вбжЊЧњЯпC![]() ЃК
ЃК![]() ЃЈtЮЊВЮЪ§ЃЉЃЌ C
ЃЈtЮЊВЮЪ§ЃЉЃЌ C![]() ЃК
ЃК![]() ЃЈ
ЃЈ![]() ЮЊВЮЪ§ЃЉЁЃ
ЮЊВЮЪ§ЃЉЁЃ
ЃЈ1ЃЉЛЏC![]() ЃЌC
ЃЌC![]() ЕФЗНГЬЮЊЦеЭЈЗНГЬЃЌВЂЫЕУїЫќУЧЗжБ№БэЪОЪВУДЧњЯпЃЛ
ЕФЗНГЬЮЊЦеЭЈЗНГЬЃЌВЂЫЕУїЫќУЧЗжБ№БэЪОЪВУДЧњЯпЃЛ
ЃЈ2ЃЉШєC![]() ЩЯЕФЕуPЖдгІЕФВЮЪ§ЮЊ
ЩЯЕФЕуPЖдгІЕФВЮЪ§ЮЊ![]() ЃЌQЮЊC
ЃЌQЮЊC![]() ЩЯЕФЖЏЕуЃЌЧѓ
ЩЯЕФЖЏЕуЃЌЧѓ![]() жаЕу
жаЕу![]() ЕНжБЯп
ЕНжБЯп
![]() ЃЈtЮЊВЮЪ§ЃЉОрРыЕФзюаЁжЕЁЃ
ЃЈtЮЊВЮЪ§ЃЉОрРыЕФзюаЁжЕЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкШчЭМЫљЪОЕФВЛЙцдђМИКЮЬхжаЃЌвбжЊЫФБпаЮ![]() ЪЧе§ЗНаЮЃЌЫФБпаЮ
ЪЧе§ЗНаЮЃЌЫФБпаЮ![]() ЪЧЦНааЫФБпаЮЃЌЦНУц
ЪЧЦНааЫФБпаЮЃЌЦНУц![]() ЦНУц
ЦНУц![]() ЃЌ
ЃЌ![]() .
.

ЃЈ1ЃЉжЄУїЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЧѓжБЯп![]() гыЦНУц
гыЦНУц![]() ЫљГЩНЧЕФе§ЧажЕ.
ЫљГЩНЧЕФе§ЧажЕ.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com