
【题目】已知数列![]() 的首项
的首项![]() ,
,![]() 是数列
是数列![]() 的前
的前![]() 项和,且满足
项和,且满足![]() .
.
(1)若数列![]() 是等差数列,求
是等差数列,求![]() 的值;
的值;
(2)确定![]() 的取值集合
的取值集合![]() ,使
,使![]() 时,数列
时,数列![]() 是递增数列.
是递增数列.
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】已知右焦点为![]() 的椭圆
的椭圆![]() 关于直线
关于直线![]() 对称的图形过坐标原点.
对称的图形过坐标原点.
![]() 是椭圆
是椭圆![]() 的左顶点,斜率为
的左顶点,斜率为![]() 的直线交
的直线交![]() 于
于![]() ,
,![]() 两点,点
两点,点![]() 在
在![]() 上,
上,![]() .
.
(Ⅰ)当![]() 时,求
时,求![]() 的面积;
的面积;
(Ⅱ)当![]() 时,证明:
时,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】被嘉定著名学者钱大昕赞誉为“国朝算学第一”的清朝数学家梅文鼎曾创造出一类“方灯体”,“灯者立方去其八角也”,如图所示,在棱长为![]() 的正方体
的正方体![]() 中,点
中,点![]() 为棱上的四等分点.
为棱上的四等分点.

(1)求该方灯体的体积;
(2)求直线![]() 和
和![]() 的所成角;
的所成角;
(3)求直线![]() 和平面
和平面![]() 的所成角.
的所成角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂拟制造一个如图所示的容积为36π立方米的有盖圆锥形容器.
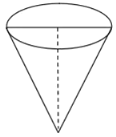
(1)若该容器的底面半径为6米,求该容器的表面积;
(2)当容器的高为多少米时,制造该容器的侧面用料最省?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】.口袋中有质地、大小完全相同的5个球,编号分别为1,2,3,4,5,甲、乙两人玩一种游戏:甲先摸出一个球,记下编号,放回后乙再摸一个球,记下编号,如果两个编号的和为偶数算甲赢,否则算乙赢.
(Ⅰ)求甲赢且编号的和为6的事件发生的概率;
(Ⅱ)这种游戏规则公平吗?试说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,![]() 是定义域为
是定义域为![]() 的奇函数.
的奇函数.
(1)确定![]() 的值;
的值;
(2)若![]() ,函数
,函数![]() ,
,![]() ,求
,求![]() 的最小值;
的最小值;
(3)若![]() ,是否存在正整数
,是否存在正整数![]() ,使得
,使得![]() 对
对![]() 恒成立?若存在,请求出所有的正整数
恒成立?若存在,请求出所有的正整数![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com