
【题目】函数f(x)=(sinx+cosx)2![]() cos(2x+π).
cos(2x+π).
(1)求函数f(x)的最小正周期;
(2)已知△ABC的内角A,B,C的对边分别为a,b,c,若![]() ,且a=2,求△ABC的面积.
,且a=2,求△ABC的面积.
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,对于函数
,对于函数![]() 有下述四个结论:
有下述四个结论:
①函数![]() 在其定义域上为增函数;
在其定义域上为增函数;
②对于任意的![]() ,都有
,都有![]() 成立;
成立;
③![]() 有且仅有两个零点;
有且仅有两个零点;
④若![]() 在点
在点![]() 处的切线也是
处的切线也是![]() 的切线,则
的切线,则![]() 必是
必是![]() 零点.
零点.
其中所有正确的结论序号是( )
A.①②③B.①②C.②③④D.②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公园计划在矩形空地上建造一个扇形花园如图①所示,矩形![]() 的
的![]() 边与
边与![]() 边的长分别为48米与40米,扇形的圆心
边的长分别为48米与40米,扇形的圆心![]() 为
为![]() 中点,扇形的圆弧端点
中点,扇形的圆弧端点![]() ,
,![]() 分别在
分别在![]() 与
与![]() 上,圆弧的中点
上,圆弧的中点![]() 在
在![]() 上.
上.
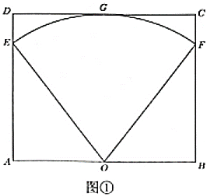
(1)求扇形花园的面积(精确到1平方米);
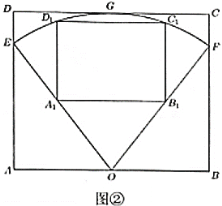
(2)若在扇形花园内开辟出一个矩形区域![]() 为花卉展览区.如图②所示,矩形
为花卉展览区.如图②所示,矩形![]() 的四条边与矩形
的四条边与矩形![]() 的对应边平行,点
的对应边平行,点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上,点
上,点![]() ,
,![]() 在扇形的弧上.某同学猜想:当矩形
在扇形的弧上.某同学猜想:当矩形![]() 面积最大时,两矩形
面积最大时,两矩形![]() 与
与![]() 的形状恰好相同(即长与宽之比相同),试求花卉展览区
的形状恰好相同(即长与宽之比相同),试求花卉展览区![]() 面积的最大值,并判断上述猜想是否正确(请说明理由).
面积的最大值,并判断上述猜想是否正确(请说明理由).
查看答案和解析>>
科目:高中数学 来源: 题型:
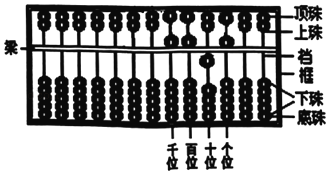
【题目】珠算被誉为中国的第五大发明,最早见于汉朝徐岳撰写的《数术记遗》2013年联合国教科文组织正式将中国珠算项目列入教科文组织人类非物质文化遗产.如图,我国传统算盘每一档为两粒上珠,五粒下珠,也称为“七珠算盘”.未记数(或表示零)时,每档的各珠位置均与图中最左档一样;记数时,要拨珠靠梁,一个上珠表示“5”,一个下珠表示“1”,例如:当千位档一个上珠、百位档一个上珠、十位档一个下珠、个位档一个上珠分别靠梁时,所表示的数是5515.现选定“个位档”、“十位档”、“百位档”和“千位档”,若规定每档拨动一珠靠梁(其它各珠不动),则在其可能表示的所有四位数中随机取一个数,这个数能被3整除的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,有一种赛车跑道类似“梨形”曲线,由圆弧![]() 和线段AB,CD四部分组成,在极坐标系Ox中,A(2,
和线段AB,CD四部分组成,在极坐标系Ox中,A(2,![]() ),B(1,
),B(1,![]() ),C(1,
),C(1,![]() ),D(2,
),D(2,![]() ),弧
),弧![]() 所在圆的圆心分别是(0,0),(2,0),曲线M1是弧
所在圆的圆心分别是(0,0),(2,0),曲线M1是弧![]() ,曲线M2是弧
,曲线M2是弧![]() .
.
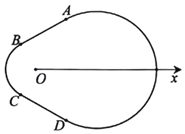
(1)分别写出M1,M2的极坐标方程:
(2)点E,F位于曲线M2上,且![]() ,求△EOF面积的取值范围.
,求△EOF面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)为奇函数,且当x≥0时,f(x)=ex﹣cosx,则不等式f(2x﹣1)+f(x﹣2)>0的解集为( )
A.(﹣∞,1)B.(﹣∞,![]() )C.(
)C.(![]() ,+∞)D.(1,+∞)
,+∞)D.(1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型公司为了切实保障员工的健康安全,贯彻好卫生防疫工作的相关要求,决定在全公司范围内举行一次乙肝普查.为此需要抽验669人的血样进行化验,由于人数较多,检疫部门制定了下列两种可供选择的方案.
方案一:将每个人的血分别化验,这时需要验669次.
方案二:按![]() 个人一组进行随机分组,把从每组
个人一组进行随机分组,把从每组![]() 个人抽来的血混合在一起进行检验,如果每个人的血均为阴性,则验出的结果呈阴性,这
个人抽来的血混合在一起进行检验,如果每个人的血均为阴性,则验出的结果呈阴性,这![]() 个人的血就只需检验一次(这时认为每个人的血化验
个人的血就只需检验一次(这时认为每个人的血化验![]() 次);否则,若呈阳性,则需对这
次);否则,若呈阳性,则需对这![]() 个人的血样再分别进行一次化验,这时该组
个人的血样再分别进行一次化验,这时该组![]() 个人的血总共需要化验
个人的血总共需要化验![]() 次.
次.
假设此次普查中每个人的血样化验呈阳性的概率为![]() ,且这些人之间的试验反应相互独立.
,且这些人之间的试验反应相互独立.
(1)设方案二中,某组![]() 个人中每个人的血化验次数为
个人中每个人的血化验次数为![]() ,求
,求![]() 的分布列.
的分布列.
(2)设![]() ,试比较方案二中,
,试比较方案二中,![]() 分别取2,3,4时,各需化验的平均总次数;并指出在这三种分组情况下,相比方案一,化验次数最多可以平均减少多少次?(最后结果四舍五入保留整数)
分别取2,3,4时,各需化验的平均总次数;并指出在这三种分组情况下,相比方案一,化验次数最多可以平均减少多少次?(最后结果四舍五入保留整数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com