
【题目】在△ABC中,角A,B,C所对边分别为a,b,c.若![]() ,c=6,则△ABC外接圆的半径大小是_____.
,c=6,则△ABC外接圆的半径大小是_____.
【答案】![]()
【解析】
由题意结合三角函数恒等变换、正弦定理可得sinBcosC=sinBsinC,结合sinB>0,可求tanC=1,结合范围C∈(0,π),可求![]() ,设△ABC外接圆的半径大小为R,根据正弦定理即可求解△ABC外接圆的半径,即可得解.
,设△ABC外接圆的半径大小为R,根据正弦定理即可求解△ABC外接圆的半径,即可得解.
由条件知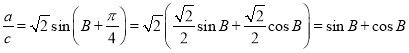 ,
,
根据正弦定理得:![]() ,
,
所以sinA=sinC(sinB+cosB)=sinCsinB+sinCcosB,
又sinA=sin(B+C)=sinBcosC+cosBsinC,
于是sinBcosC=sinBsinC,
因为sinB>0,所以cosC=sinC即tanC=1,
又C∈(0,π),所以![]() ,
,
设△ABC外接圆的半径大小为R,根据正弦定理得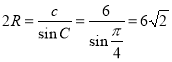 ,
,
因此![]() .
.
故答案为:![]() .
.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:高中数学 来源: 题型:
【题目】近年来,共享单车在我国各城市迅猛发展,为人们的出行提供了便利,但也给城市的交通管理带来了一些困难,为掌握共享单车在![]() 省的发展情况,某调查机构从该省抽取了5个城市,并统计了共享单车的
省的发展情况,某调查机构从该省抽取了5个城市,并统计了共享单车的![]() 指标
指标![]() 和
和![]() 指标
指标![]() ,数据如下表所示:
,数据如下表所示:
城市1 | 城市2 | 城市3 | 城市4 | 城市5 | |
| 2 | 4 | 5 | 6 | 8 |
| 3 | 4 | 4 | 4 | 5 |
(1)试求![]() 与
与![]() 间的相关系数
间的相关系数![]() ,并说明
,并说明![]() 与
与![]() 是否具有较强的线性相关关系(若
是否具有较强的线性相关关系(若![]() ,则认为
,则认为![]() 与
与![]() 具有较强的线性相关关系,否则认为没有较强的线性相关关系).
具有较强的线性相关关系,否则认为没有较强的线性相关关系).
(2)建立![]() 关于
关于![]() 的回归方程,并预测当
的回归方程,并预测当![]() 指标为7时,
指标为7时,![]() 指标的估计值.
指标的估计值.
(3)若某城市的共享单车![]() 指标
指标![]() 在区间
在区间![]() 的右侧,则认为该城市共享单车数量过多,对城市的交通管理有较大的影响交通管理部门将进行治理,直至
的右侧,则认为该城市共享单车数量过多,对城市的交通管理有较大的影响交通管理部门将进行治理,直至![]() 指标
指标![]() 在区间
在区间![]() 内现已知
内现已知![]() 省某城市共享单车的
省某城市共享单车的![]() 指标为13,则该城市的交通管理部门是否需要进行治理?试说明理由.
指标为13,则该城市的交通管理部门是否需要进行治理?试说明理由.
参考公式:回归直线![]() 中斜率和截距的最小二乘估计分别为
中斜率和截距的最小二乘估计分别为
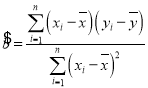 ,,
,,![]() 相关系数
相关系数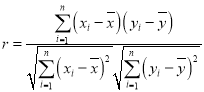
参考数据: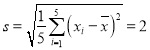 ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在直角梯形![]() 中,
中,![]() ,
,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上的点,
上的点,![]() ,且
,且![]() (如图①).将四边形
(如图①).将四边形![]() 沿
沿![]() 折起,连接
折起,连接![]() 、
、![]() 、
、![]() (如图②).在折起的过程中,则下列表述:
(如图②).在折起的过程中,则下列表述:

①![]() 平面
平面![]() ;
;
②四点![]() 、
、![]() 、
、![]() 、
、![]() 可能共面;
可能共面;
③若![]() ,则平面
,则平面![]() 平面
平面![]() ;
;
④平面![]() 与平面
与平面![]() 可能垂直.其中正确的是__________.
可能垂直.其中正确的是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
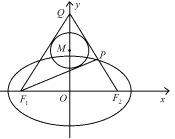
【题目】如图,已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,
,![]() ,
,![]() 是
是![]() 轴的正半轴上一点,
轴的正半轴上一点,![]() 交椭圆于
交椭圆于![]() ,且
,且![]() ,
,![]() 的内切圆
的内切圆![]() 半径为1.
半径为1.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() 点为圆
点为圆![]() 上一点,求
上一点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)![]() sin(ωx+φ)﹣cos(ωx+φ)(0<φ<π,ω>0)为偶函数,且y=f(x)图象的两相邻对称轴间的距离为
sin(ωx+φ)﹣cos(ωx+φ)(0<φ<π,ω>0)为偶函数,且y=f(x)图象的两相邻对称轴间的距离为![]() ,则f(
,则f(![]() )的值为( )
)的值为( )
A.﹣1B.1C.![]() .D.
.D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为实常数且
为实常数且![]() ).
).
(Ⅰ)当![]() 时;
时;
①设![]() ,判断函数
,判断函数![]() 的奇偶性,并说明理由;
的奇偶性,并说明理由;
②求证:函数![]() 在
在![]() 上是增函数;
上是增函数;
(Ⅱ)设集合![]() ,若
,若![]() ,求
,求![]() 的取值范围(用
的取值范围(用![]() 表示).
表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
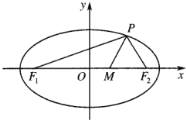
【题目】已知椭圆![]() 的左、右焦点分别是
的左、右焦点分别是![]() ,
,![]() ,点
,点![]() 是椭圆
是椭圆![]() 上除长轴端点外的任一点,连接
上除长轴端点外的任一点,连接![]() ,
,![]() ,设
,设![]() 的内角平分线
的内角平分线![]() 交
交![]() 的长轴于点
的长轴于点![]() .
.
(Ⅰ)求实数![]() 的取值范围;
的取值范围;
(Ⅱ)求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com