
已知椭圆![]() 经过点(0
经过点(0![]() ,
,![]() ),离心率为
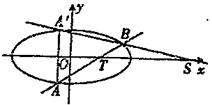
),离心率为![]() ,经过椭圆C的右焦点F的直线l交椭圆于A、B两点,点A、F、B在直线x=4上的射影依次为点D、K、E.
,经过椭圆C的右焦点F的直线l交椭圆于A、B两点,点A、F、B在直线x=4上的射影依次为点D、K、E.
(1)求椭圆C的方程;
(2)若直线l交y轴于点M,且![]() ,当直线l
,当直线l![]() 的倾斜角变化时,探求
的倾斜角变化时,探求![]() 的值是否为定值?若
的值是否为定值?若![]() 是,求出
是,求出![]() 的值,否则,说明理由;
的值,否则,说明理由;
(3)连接AE、BD,试探索当直线l的倾斜角变化时,直线AE与BD是否相交于定点?若是,请求出定点的坐标,并给予证明;否则,说明理由.
.解:(Ⅰ)易知![]() 因为
因为![]()
![]() ∴椭圆C的方程
∴椭圆C的方程![]() …………………………3分
…………………………3分
(2)易知直线l的斜率存在,设直线l方程![]() 且l
且l![]() 与y轴交于
与y轴交于![]() 设直线l交椭圆于
设直线l交椭圆于![]()
由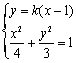 得
得![]()
![]() ……………………………………6分
……………………………………6分
又由![]()
![]() ,同理
,同理![]() …………………
…………………![]() ………………………8分
………………………8分
![]()
所以当直线l的倾斜角变化时,![]() 的值为定值-
的值为定值-![]() ;…………………………10分
;…………………………10分
(3)当直线l斜率不存在时,直线![]() 轴,则ABED为矩形,由对称性知,AE与BD相交FK的中点N(
轴,则ABED为矩形,由对称性知,AE与BD相交FK的中点N(![]() ,0),
,0),
猜想,当直线l的倾斜角变化时,AE与BD相交于定点N(![]() ,0)……………………11分
,0)……………………11分
证明:由(2)知![]()
当直线l的倾斜角变化时,首先证直线AE过定点N(![]() ,0),
,0),
![]() ∶
∶![]()
当![]() 时,
时,![]()
=![]()
=![]() 点N(
点N(![]() ,0),在直线lAE上,同理可证,点N(
,0),在直线lAE上,同理可证,点N(![]() ,0)
,0)
也在直线lBD上;∴当m变化时,AE与BD相交于定点(![]() ,0)…………14分
,0)…………14分


 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源:2013届湖北武汉部分重点中学(五校)高二下期中文科数学卷(解析版) 题型:解答题
(14分)已知椭圆 经过点(0,1),离心率
经过点(0,1),离心率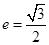 。
。
(1)求椭圆C的方程;
(2)设直线 与椭圆C交于A、B两点,点A关于x轴的对称点为
与椭圆C交于A、B两点,点A关于x轴的对称点为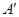 。
。
①试建立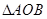 的面积关于m的函数关系;
的面积关于m的函数关系;
②某校高二(1)班数学兴趣小组通过试验操作初步推断;“当m变化时,直线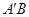 与x轴交于一个定点”。你认为此推断是否正确?若正确,请写出定点坐标,并证明你的结论;若不正确,请说明理由。
与x轴交于一个定点”。你认为此推断是否正确?若正确,请写出定点坐标,并证明你的结论;若不正确,请说明理由。
查看答案和解析>>
科目:高中数学 来源:2011-2012学年黑龙江省高三上学期期末考试理科数学试卷 题型:解答题
已知椭圆 经过点(0,
经过点(0, ),离心率为
),离心率为 ,直线l经过椭圆C的右焦点F交椭圆于A、B两点,点A、F、B在直线x=4上的射影依次为点D、K、E.
,直线l经过椭圆C的右焦点F交椭圆于A、B两点,点A、F、B在直线x=4上的射影依次为点D、K、E.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若直线l交y轴于点M,且 ,当直线l的倾斜角变化时,探求
,当直线l的倾斜角变化时,探求 的值是否为定值?若是,求出
的值是否为定值?若是,求出 的值,否则,说明理由;
的值,否则,说明理由;
(Ⅲ)连接AE、BD,试探索当直线l的倾斜角变化时,直线AE与BD是否相交于定点?若是,请求出定点的坐标,并给予证明;否则,说明理由.

查看答案和解析>>
科目:高中数学 来源:2010-2011学年浙江省高三上学期期中考试数学文卷 题型:解答题
(本小题满分15分)已知椭圆 经过点(0,1),离心率
经过点(0,1),离心率
(I)求椭圆C的方程;
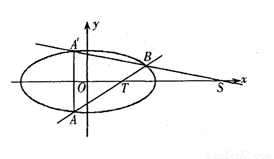
(II)设直线 与椭圆C交于A,B两点,点A关于x轴的对称点为A’.试问:当m变化时直线
与椭圆C交于A,B两点,点A关于x轴的对称点为A’.试问:当m变化时直线 与x轴是否交于一个定点?若是,请写出定点坐标,并证明你的结论;若不是,请说明理由。
与x轴是否交于一个定点?若是,请写出定点坐标,并证明你的结论;若不是,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分13分)已知椭圆![]() 经过点(0,
经过点(0,![]() ),离心率为
),离心率为![]() ,直线l经过椭圆C的右焦点F交椭圆于A、B两点,点A、F、B在直线x=4上的射影依次为点D、K、E.
,直线l经过椭圆C的右焦点F交椭圆于A、B两点,点A、F、B在直线x=4上的射影依次为点D、K、E.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若直线l交y轴于点M,且![]() ,当直线l的倾斜角变化时,探求
,当直线l的倾斜角变化时,探求![]() 的值是否为定值?若是,求出
的值是否为定值?若是,求出![]() 的值,否则,说明理由;
的值,否则,说明理由;
(Ⅲ)连接AE、BD,试探索当直线l的倾斜角变化时,直线AE与BD是否相交于定点?若是,请求出定点的坐标,并给予证明;否则,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分14分)
已知椭圆![]() 经过点(0,
经过点(0,![]() ),离心率为
),离心率为![]() ,经过椭圆C的右焦点F的直线l交椭圆于A、B两点,点A、F、B在直线x=4上的射影依次为点D、K、E.
,经过椭圆C的右焦点F的直线l交椭圆于A、B两点,点A、F、B在直线x=4上的射影依次为点D、K、E.
(1)求椭圆C的方程;
(2)若直线l交y轴于点M,且![]() ,当直线l的倾斜角变化时,探求
,当直线l的倾斜角变化时,探求![]() 的值是否为定值?若是,求出
的值是否为定值?若是,求出![]() 的值,否则,说明理由;
的值,否则,说明理由;
(3)连接AE、BD,试探索当直线l的倾斜角变化时,直线AE与BD是否相交于定点?若是,请求出定点的坐标,并给予证明;否则,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com