
【题目】已知点![]() ,点
,点![]() 在
在![]() 轴负半轴上,以
轴负半轴上,以![]() 为边做菱形
为边做菱形![]() ,且菱形
,且菱形![]() 对角线的交点在
对角线的交点在![]() 轴上,设点
轴上,设点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() ,其中
,其中![]() ,作曲线
,作曲线![]() 的切线,设切点为
的切线,设切点为![]() ,求
,求![]() 面积的取值范围.
面积的取值范围.
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点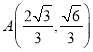 ,其左、右两个焦点分别为
,其左、右两个焦点分别为![]() ,
,![]() ,短轴的一个端点为
,短轴的一个端点为![]() ,且
,且![]() .
.
(1)求![]() 的平分线所在的直线方程;
的平分线所在的直线方程;
(2)设直线![]() :
:![]() 与椭圆交于不同的两点
与椭圆交于不同的两点![]() ,
,![]() .且
.且![]() 为坐标原点,若
为坐标原点,若![]() ,求
,求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
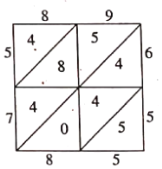
【题目】写算,是一种格子乘法,也是笔算乘法的一种,用以区别筹算与珠算,它由明代数学家吴敬在其撰写的《九章算法比类大全》一书中提出,是从天元式的乘法演变而来.例如计算![]() ,将被乘数89计入上行,乘数65计入右行.然后以乘数65的每位数字乘被乘数89的每位数字,将结果计入相应的格子中,最后从右下方开始按斜行加起来,满十向上斜行进一,如图,即得5785.类比此法画出
,将被乘数89计入上行,乘数65计入右行.然后以乘数65的每位数字乘被乘数89的每位数字,将结果计入相应的格子中,最后从右下方开始按斜行加起来,满十向上斜行进一,如图,即得5785.类比此法画出![]() 的表格,若从表内(表周边数据不算在内)任取一数,则恰取到奇数的概率是( )
的表格,若从表内(表周边数据不算在内)任取一数,则恰取到奇数的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市举行“中学生诗词大赛”,分初赛和复赛两个阶段进行,规定:初赛成绩大于90分的具有复赛资格,某校有800名学生参加了初赛,所有学生的成绩均在区间![]() 内,其频率分布直方图如图.
内,其频率分布直方图如图.

(Ⅰ)求获得复赛资格的人数;
(Ⅱ)从初赛得分在区间![]() 的参赛者中,利用分层抽样的方法随机抽取
的参赛者中,利用分层抽样的方法随机抽取![]() 人参加学校座谈交流,那么从得分在区间
人参加学校座谈交流,那么从得分在区间![]() 与
与![]() 各抽取多少人?
各抽取多少人?
(Ⅲ)从(Ⅱ)抽取的![]() 人中,选出
人中,选出![]() 人参加全市座谈交流,设
人参加全市座谈交流,设![]() 表示得分在区间
表示得分在区间![]() 中参加全市座谈交流的人数,求
中参加全市座谈交流的人数,求![]() 的分布列及数学期望E(X).
的分布列及数学期望E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,已知点
中,已知点![]() ,
,![]() ,动点
,动点![]() 满足直线
满足直线![]() 与
与![]() 的斜率之积为
的斜率之积为![]() .记
.记![]() 的轨迹为曲线
的轨迹为曲线![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 和
和![]() 的直角坐标方程;
的直角坐标方程;
(2)求![]() 上的点到
上的点到![]() 距离的最小值.
距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,墙上有一壁画,最高点![]() 离地面4米,最低点
离地面4米,最低点![]() 离地面2米,观察者从距离墙
离地面2米,观察者从距离墙![]() 米,离地面高
米,离地面高![]() 米的
米的![]() 处观赏该壁画,设观赏视角
处观赏该壁画,设观赏视角![]()

(1)若![]() 问:观察者离墙多远时,视角
问:观察者离墙多远时,视角![]() 最大?
最大?
(2)若![]() 当
当![]() 变化时,求
变化时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com