
【题目】已知函数![]() .
.
(1)若![]() ,求曲线在
,求曲线在![]() 点处的切线方程;
点处的切线方程;
(2)若曲线![]() 与直线
与直线![]() 只有一个交点,求实数
只有一个交点,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)求点![]() 处的切线方程,只要求出导数
处的切线方程,只要求出导数![]() ,则有切线方程为
,则有切线方程为![]() ;(2)曲线
;(2)曲线![]() 与直线
与直线![]() 只有一个交点,说明关于
只有一个交点,说明关于![]() 的方程
的方程![]() 只有一个实根,
只有一个实根,![]() 不可能是根,因此方程可转化为方程
不可能是根,因此方程可转化为方程![]() 只有一个实根,这样问题又转化为函数
只有一个实根,这样问题又转化为函数![]() 的图象与直线
的图象与直线![]() 只有一个交点,因此只要研究函数
只有一个交点,因此只要研究函数![]() 的单调性,极值,函数值变化情况,作出简图就可得出结论.
的单调性,极值,函数值变化情况,作出简图就可得出结论.
试题解析:(1)![]() ,
,![]() ,
,![]() ,所以切线方程为
,所以切线方程为![]() .
.
(2)曲线![]() 与直线
与直线![]() 只有一个交点,等价于关于
只有一个交点,等价于关于![]() 的方程
的方程![]() 只有一个实根.
只有一个实根.
显然![]() ,所以方程
,所以方程![]() 只有一个实根.
只有一个实根.
设函数![]() ,则
,则![]() .
.
设![]() ,
,![]() ,
,![]() 为增函数,又
为增函数,又![]() .
.
所以当![]() 时,
时,![]() ,
,![]() 为增函数;
为增函数;
当![]() 时,
时,![]() ,
,![]() 为减函数;
为减函数;
当![]() 时,
时,![]() ,
,![]() 为增函数;
为增函数;
所以![]() 在
在![]() 时取极小值
时取极小值![]() .
.
又当![]() 趋向于
趋向于![]() 时,
时,![]() 趋向于正无穷;
趋向于正无穷;
又当![]() 趋向于负无穷时,
趋向于负无穷时,![]() 趋向于负无穷;
趋向于负无穷;
又当![]() 趋向于正无穷时,
趋向于正无穷时,![]() 趋向于正无穷.所以
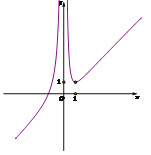
趋向于正无穷.所以![]() 图象大致如图所示:
图象大致如图所示:
所以方程![]() 只有一个实根时,实数
只有一个实根时,实数![]() 的取值范围为
的取值范围为![]() .
.


 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)的定义域为{x|x∈R,且x≠2},且y=f(x+2)是偶函数,当x<2时,f(x)=|2x﹣1|,那么当x>2时,函数f(x)的递减区间是( )
A.(3,5)
B.(3,+∞)
C.(2,+∞)
D.(2,4]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:(x﹣2)2+y2=9,直线l:x+y=0.
(1)求过圆C的圆心且与直线l垂直的直线n的方程;
(2)求与圆C相切,且与直线l平行的直线m的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题:①函数f(x)=sin2x一cos2x的最小正周期是![]() ;
;
②在等比数列〔![]() }中,若
}中,若![]() ,则a3=士2;
,则a3=士2;
③设函数f(x)=![]() ,若
,若![]() 有意义,则
有意义,则![]()
④平面四边形ABCD中, ![]() ,则四边形ABCD是
,则四边形ABCD是
菱形. 其中所有的真命题是:( )
A. ①②④ B. ①④ C. ③④ D. ①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
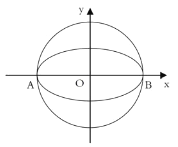
【题目】如图,椭圆![]() 的离心率为
的离心率为![]() ,其左顶点
,其左顶点![]() 在圆
在圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 与椭圆
与椭圆![]() 的另一个交点为
的另一个交点为![]() ,与圆
,与圆![]() 的另一个交点为
的另一个交点为![]() .
.
(ⅰ)当![]() 时,求直线
时,求直线![]() 的斜率;
的斜率;
(ⅱ)是否存在直线![]() ,使
,使![]() ?若存在,求出直线
?若存在,求出直线![]() 的斜率;若不存在,说明理由.
的斜率;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() ,则导函数f′(x)是( )
,则导函数f′(x)是( )
A.仅有最小值的奇函数
B.既有最大值,又有最小值的偶函数
C.仅有最大值的偶函数
D.既有最大值,又有最小值的奇函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|ax﹣1|﹣(a﹣1)x
(1)当a= ![]() 时,满足不等式f(x)>1的x的取值范围为;若函数f(x)的图象与x轴没有交点,则实数a的取值范围为 .
时,满足不等式f(x)>1的x的取值范围为;若函数f(x)的图象与x轴没有交点,则实数a的取值范围为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|logax|(0<a<1)的定义域为[m,n](m<n),值域为[0,1],若n﹣m的最小值为 ![]() ,则实数a的值为( )
,则实数a的值为( )
A.![]()
B.![]() 或
或 ![]()
C.![]()
D.![]() 或
或 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的顶点在原点,焦点在
的顶点在原点,焦点在![]() 轴上,且抛物线上有一点
轴上,且抛物线上有一点![]() 到焦点的距离为5.
到焦点的距离为5.
(1)求该抛物线![]() 的方程;
的方程;
(2)已知抛物线上一点![]() ,过点
,过点![]() 作抛物线的两条弦
作抛物线的两条弦![]() 和
和![]() ,且
,且![]() ,判断直线
,判断直线![]() 是否过定点?并说明理由.
是否过定点?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com