【题目】2019年春节档有多部优秀电影上映，其中《流浪地球》是比较火的一部.某影评网站统计了100名观众对《流浪地球》的评分情况，得到如下表格：
评价等级 | ★ | ★★ | ★★★ | ★★★★ | ★★★★★ |
分数 | 0～20 | 2140 | 4160 | 61～80 | 81100 |
人数 | 5 | 2 | 12 | 6 | 75 |
(1)根据以上评分情况，试估计观众对《流浪地球》的评价在四星以上(包括四星)的频率；
(2)以表中各评价等级对应的频率作为各评价等级对应的概率，假设每个观众的评分结果相互独立.
(i)若从全国所有观众中随机选取3名，求恰有2名评价为五星1名评价为一星的概率；
(ii)若从全国所有观众中随机选取16名，记评价为五星的人数为X，求X的方差.
愉快的寒假南京出版社系列答案科目：高中数学 来源： 题型：
【题目】已知曲线 y = x3 + x－2 在点 P0 处的切线
平行于直线
4x－y－1=0，且点 P0 在第三象限,
⑴求P0的坐标;
⑵若直线
, 且 l 也过切点P0 ,求直线l的方程.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】
某学校高一数学兴趣小组对学生每周平均体育锻炼小时数与体育成绩优秀（体育成绩满分100分，不低于85分称优秀）人数之间的关系进行分析研究，他们从本校初二，初三，高一，高二，高三年级各随机抽取了40名学生，记录并整理了这些学生周平均体育锻炼小时数与体育成绩优秀人数，得到如下数据表：
初二 | 初三 | 高一 | 高二 | 高三 | |
周平均体育锻炼小时数工（单位：小时） | 14 | 11 | 13 | 12 | 9 |
体育成绩优秀人数y（单位：人） | 35 | 26 | 32 | 26 | 19 |
该兴趣小组确定的研究方案是：先从这5组数据中选取3组数据求线性回归方程，再用剩下的2组数据进行检验.
（1）若选取的是初三，高一，高二的3组数据，请根据这3组数据，求出y关于x的线性回归方程
；
（2）若由线性回归方程得到的估计数据与所选取的检验数据的误差均不超过1，则认为得到的线性回归方程是可靠的，试问（1）中所得到的线性回归方程是否可靠？
参考数据：
，
.
参考公式：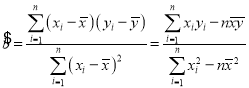
，
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】我国古代数学名著《九章算术》里有一道关于玉石的问题：“今有玉方一寸，重七两;石方一寸，重六两.今有石方三寸，中有玉，并重十一斤（176两）问玉、石重各几何？”如图所示的程序框图反映了对此题的一个求解算法，运行该程序框图，则输出的
，
分别为( )
A.98，78B.96，80C.94，74D.92，72
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
.
（1）若函数
在
上是增函数，求正数
的取值范围；
（2）当
时，设函数的图象与x轴的交点为
，
，曲线
在，两点处的切线斜率分别为
，
，求证：+ 
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆E:
的焦点在
轴上，A是E的左顶点，斜率为k （k > 0）的直线交E于A，M两点，点N在E上，MA⊥NA.
（Ⅰ）当t=4，
时，求△AMN的面积；
（Ⅱ）当
时，求k的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列有关命题的说法正确的是（ ）
A. 
，使得
成立．
B. 命题
：任意
，都有
，则
：存在
，使得
．
C. 命题“若
且
，则
且
”的逆命题为真命题．
D. 若数列
是等比数列，
则
是
的必要不充分条件．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某校高一年级模仿《中国诗词大会》节目举办学校诗词大会，进入正赛的条件为：电脑随机抽取10首古诗，参赛者能够正确背诵6首及以上的进入正赛，若学生甲参赛，他背诵每一首古诗的正确的概率均为
(1)求甲进入正赛的概率；
(2)若进入正赛，则采用积分淘汰制，规则是：电脑随机抽取4首古诗，每首古诗背诵正确加2分，错误减1分.由于难度增加，甲背诵每首古诗正确的概率为
，求甲在正赛中积分
的概率分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
