
【题目】已知函数![]() .
.
(1)若函数![]() 与
与![]() 的图象恰好相切与点
的图象恰好相切与点![]() ,求实数
,求实数![]() 的值;
的值;
(2)当![]() 时,
时, ![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)求证: ![]() .
.
【答案】(1)![]() (2)
(2)![]() (3)见解析
(3)见解析
【解析】试题分析:(1)根据导数几何意义得![]() ,即得实数
,即得实数![]() 的值;(2)利用分参法将不等式恒成立问题转化为对应函数最值问题
的值;(2)利用分参法将不等式恒成立问题转化为对应函数最值问题![]() (x>1)最大值,再利用导数研究函数
(x>1)最大值,再利用导数研究函数![]() 单调性:单调递减,最后根据洛必达法则求最大值,即得实数
单调性:单调递减,最后根据洛必达法则求最大值,即得实数![]() 的取值范围(3)先根据和的关系转化为对应项的关系:
的取值范围(3)先根据和的关系转化为对应项的关系: ![]() ,再利用(2)的结论
,再利用(2)的结论![]() ,令
,令![]() ,则代入放缩得证
,则代入放缩得证
试题解析:(1)![]()
所以![]()
(2)方法一:(分参)
即![]() 时,
时, ![]() ,
, ![]() 时,显然成立;
时,显然成立;
![]() 时,即
时,即![]()
令![]() ,则
,则
令![]() []
[]
![]()
![]() 即
即![]()
![]() 在
在![]() 上单调递减
上单调递减
![]()
故![]()
方法二:(先找必要条件)
注意到![]() 时,恰有
时,恰有![]()
令![]()
则
![]() 在
在![]() 恒成立的必要条件为
恒成立的必要条件为![]()
即![]()
下面证明:当![]() 时,
时, ![]()

令![]()
![]() 即
即![]()
![]() 在
在![]() 递减,
递减,
![]() 恒成立,即
恒成立,即![]() 也是充分条件,故有
也是充分条件,故有![]() .
.
(3)不妨设![]() 为
为![]() 前
前![]() 项和,则
项和,则![]()
要证原不等式,只需证![]()
而由(2)知:当![]() 时恒有
时恒有![]()
即![]() 当且仅当
当且仅当![]() 时取等号
时取等号
取![]() ,则
,则
即![]() 即
即![]()
即![]() 成立,从而原不等式获证.
成立,从而原不等式获证.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案科目:高中数学 来源: 题型:
【题目】已知两直线l1:x+8y+7=0和l2:2x+y﹣1=0.
(1)求l1与l2交点坐标;
(2)求过l1与l2交点且与直线x+y+1=0平行的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出如下几个结论:①命题“x∈R,sinx+cosx=2”的否定是“x∈R,sinx+cosx≠2”;②命题“x∈R,sinx+ ![]() ≥2”的否定是“x∈R,sinx+
≥2”的否定是“x∈R,sinx+ ![]() <2”;③对于x∈(0,
<2”;③对于x∈(0, ![]() ),tanx+
),tanx+ ![]() ≥2;
≥2;
④x∈R,使sinx+cosx= ![]() .其中正确的为( )
.其中正确的为( )
A.③
B.③④
C.②③④
D.①②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,曲线![]() 的方程为
的方程为![]() .以坐标原点为极点,
.以坐标原点为极点, ![]() 轴的非负半轴为极轴,建立极坐标系,曲线
轴的非负半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的参数方程和曲线
的参数方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 在曲线
在曲线![]() 上,点
上,点![]() 在曲线
在曲线![]() 上,求
上,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的![]() 分别为14,18,则输出的
分别为14,18,则输出的![]() 为( )
为( )
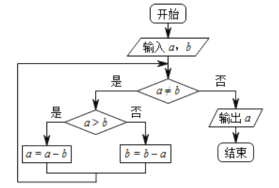
A. 0 B. 2 C. 4 D. 14
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校在2013年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[160,165),第2组[165,170),第3组[170,175),第4组[175,180),第5组[180,85],得到的频率分布直方图如图所示.
(1)求第3,4,5组的频率;
(2)为了能选拔出最优秀的学生,该校决定在笔试成绩高的第3,4,5组中用分层抽样的方法抽取6名学生进入第二轮面试,求第3,4,5组每组各抽取多少名学生进入第二轮面试?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】北京时间3月15日下午,谷歌围棋人工智能![]() 与韩国棋手李世石进行最后一轮较量,
与韩国棋手李世石进行最后一轮较量,![]() 获得本场比赛胜利,最终人机大战总比分定格在
获得本场比赛胜利,最终人机大战总比分定格在![]() .人机大战也引发全民对围棋的关注,某学校社团为调查学生学习围棋的情况,随机抽取了100名学生进行调查.根据调查结果绘制的学生日均学习围棋时间的频率分布直方图(如图所示),将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.
.人机大战也引发全民对围棋的关注,某学校社团为调查学生学习围棋的情况,随机抽取了100名学生进行调查.根据调查结果绘制的学生日均学习围棋时间的频率分布直方图(如图所示),将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.
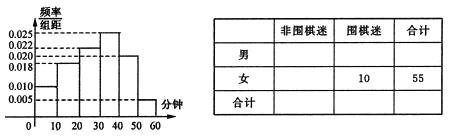
(1)根据已知条件完成如图列联表,并据此资料判断你是否有![]() 的把握认为“围棋迷”与性别有关?
的把握认为“围棋迷”与性别有关?
(2)将上述调查所得到的频率视为概率.现在从该地区大量学生中,采用随机抽样方法每次抽取1名学生,抽取3次,记所抽取的3名学生中的“围棋迷”人数为![]() .若每次抽取的结果是相互独立的,求
.若每次抽取的结果是相互独立的,求![]() 的分布列,期望
的分布列,期望![]() 和方差
和方差![]() .
.
附:![]() ,其中
,其中![]() .
.
| 0.05 | 0.010 |
| 3.74 | 6.63 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com