
【题目】如图四棱锥![]() 中,
中,![]() 底面
底面![]() ,
,![]() 是边长为2的等边三角形,且
是边长为2的等边三角形,且![]() ,
,![]() ,点
,点![]() 是棱
是棱![]() 上的动点.
上的动点.
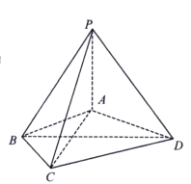
(I)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)当线段![]() 最小时,求直线
最小时,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(I)证明见解析;(Ⅱ)![]() .
.
【解析】
(Ⅰ)由![]() 底面
底面![]() 可得
可得![]() .取
.取![]() 的中点
的中点![]() ,连接
,连接![]() ,根据等腰三角形的性质可得
,根据等腰三角形的性质可得![]() ,于是得到
,于是得到![]() 平面
平面![]() ,根据面面垂直的判定可得所证结论.(Ⅱ)取
,根据面面垂直的判定可得所证结论.(Ⅱ)取![]() 中点
中点![]() ,连接
,连接![]() ,可证得
,可证得![]() ,建立空间直角坐标系.然后根据向量的共线得到点
,建立空间直角坐标系.然后根据向量的共线得到点![]() 的坐标,再根据线段
的坐标,再根据线段![]() 最短得到点
最短得到点![]() 的位置,进而得到
的位置,进而得到![]() .求出平面
.求出平面![]() 的法向量后根据线面角与向量夹角间的关系可得所求.
的法向量后根据线面角与向量夹角间的关系可得所求.
(Ⅰ)证明:∵![]() 底面
底面![]() ,
,![]() 底面
底面![]() ,
,
∴![]() .
.
取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,
∵![]() 是等边三角形,
是等边三角形,![]() ,
,
∴![]() ,
,![]() ,
,
∴点![]() 共线,从而得
共线,从而得![]() ,
,
又![]() ,
,
∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .
.
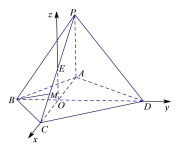
(Ⅱ)解:取![]() 中点
中点![]() ,连接
,连接![]() ,则
,则![]() ,
,
∴![]() 底面
底面![]() ,
,
∴![]() 两两垂直.
两两垂直.
以![]() 为原点如图建立空间直角坐标系
为原点如图建立空间直角坐标系![]() ,
,
则![]() ,
,
∴![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
由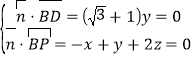 ,得
,得![]() ,
,
令![]() ,得
,得![]() .
.
设![]() ,则
,则![]() ,
,
∴![]() ,
,
∴当![]() 时,
时,![]() 有最小值,且
有最小值,且![]() ,此时
,此时![]() .
.
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
则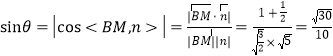 ,
,
∴直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程与曲线
的普通方程与曲线![]() 直角坐标方程;
直角坐标方程;
(2)设![]() 为曲线
为曲线![]() 上的动点,求点
上的动点,求点![]() 到
到![]() 上点的距离的最小值,并求此时点
上点的距离的最小值,并求此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的离心率为
的离心率为![]() ,且经过点M(1,
,且经过点M(1,![]() ).
).
(1)求椭圆C的标准方程;
(2)已知直线l不过点P(0,1),与椭圆C交于A、B两点,记直线PA、PB的斜率分别为k1、k2,且满足k1+k2=1,求证:直线l过定点,并求出该定点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“中国剩余定理”又称“孙子定理”.1852年英国来华传教士伟烈亚力将《孙子算经》中“物不知数”问题的解法传至欧洲.1874年英国数学家马西森指出此法符合1801年由高斯得到的关于同余式解法的一般性定理,因而西方称之为“中国剩余定理”,“中国剩余定理”讲的是一个关于整除的问题,现有这样一个整除问题:将1到2030这2030个自然数中,能被3除余1且被4除余1的数按从小到大的顺序排成一列,构成数列![]() ,则此数列共有( )
,则此数列共有( )
A.168项B.169项C.170项D.171项
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以
为参数),以![]() 轴的非负半轴为极轴,原点
轴的非负半轴为极轴,原点![]() 为极点建立极坐标系,两种坐标系中取相同的长度单位,若直线
为极点建立极坐标系,两种坐标系中取相同的长度单位,若直线![]() 和
和![]()
![]() 分别与曲线
分别与曲线![]() 相交于
相交于![]() 、
、![]() 两点(
两点(![]() ,
,![]() 两点异于坐标原点).
两点异于坐标原点).
(1)求曲线![]() 的普通方程与
的普通方程与![]() 、
、![]() 两点的极坐标;
两点的极坐标;
(2)求直线![]() 的极坐标方程及
的极坐标方程及![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的左焦点为
的左焦点为![]() ,离心率为
,离心率为![]() ,
,![]() 为圆
为圆![]() 的圆心.
的圆心.
(1)求椭圆的方程;
(2)已知过椭圆右焦点![]() 的直线
的直线![]() 交椭圆于
交椭圆于![]() 两点,过
两点,过![]() 且与
且与![]() 垂直的直线
垂直的直线![]() 与圆
与圆![]() 交于
交于![]() 两点,求四边形
两点,求四边形![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知六棱锥![]() 的底面是正六边形,
的底面是正六边形,![]() 平面ABC,
平面ABC,![]() .则下列命题中正确的有( )
.则下列命题中正确的有( )
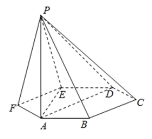
①平面![]() 平面PAE;
平面PAE;
②![]() ;
;
③直线CD与PF所成角的余弦值为![]() ;
;
④直线PD与平面ABC所成的角为45°;
⑤![]() 平面PAE.
平面PAE.
A.①④B.①③④C.②③⑤D.①②④⑤
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知偶函数![]() 满足
满足![]() ,现给出下列命题:①函数
,现给出下列命题:①函数![]() 是以2为周期的周期函数;②函数
是以2为周期的周期函数;②函数![]() 是以4为周期的周期函数;③函数
是以4为周期的周期函数;③函数![]() 为奇函数;④函数
为奇函数;④函数![]() 为偶函数,则其中真命题的个数是( )
为偶函数,则其中真命题的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com