
【题目】四棱锥![]() 中,底面
中,底面![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() 为
为![]() 中点.
中点.
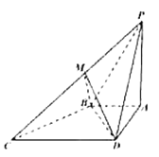
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见证明;(2) ![]()
【解析】
(1)在![]() 中,由余弦定理,
中,由余弦定理,![]() ,又
,又![]() ,
,![]() ,得到
,得到![]() ,
,![]() ,
,
由线面垂直的判定定理,得![]() 平面
平面![]() ,进而利用面面垂直的判定定理,证得平面
,进而利用面面垂直的判定定理,证得平面![]() 平面
平面![]() .
.
(2)以![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 为
为![]() ,
,![]() ,
,![]() 轴,建立空间直角坐标系,求得平面
轴,建立空间直角坐标系,求得平面![]() 的法向量为
的法向量为![]() 和平面平面
和平面平面![]() 的一个法向量为
的一个法向量为![]() ,利用向量的夹角公式,即可求解.
,利用向量的夹角公式,即可求解.
(1)在直角梯形中,![]() ,
,![]() ,
,
在![]() 中,由余弦定理,
中,由余弦定理,![]() ,又
,又![]() ,
,![]() ,
,
有![]() ,
,![]() 是等腰三角形,所以
是等腰三角形,所以![]() ,
,![]() ,
,
由线面垂直的判定定理,得![]() 平面
平面![]() ,
,
又由面面垂直的判定定理,即可得到平面![]() 平面
平面![]() .
.
(2)以![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 为
为![]() ,
,![]() ,
,![]() 轴,建立空间直角坐标系,
轴,建立空间直角坐标系,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
有![]() ,
,![]() ,
,![]() ,
,
令平面![]() 的法向量为
的法向量为![]() ,由
,由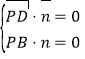 ,可得一个
,可得一个![]() ,
,
由(1)可知平面![]() 的一个法向量为
的一个法向量为![]() ,
,
所以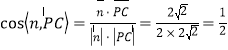 ,
,
所以二面角![]() 的余弦值为
的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】![]() 义乌国际马拉松赛,某校要从甲乙丙丁等
义乌国际马拉松赛,某校要从甲乙丙丁等![]() 人中挑选
人中挑选![]() 人参加比赛,其中甲乙丙丁
人参加比赛,其中甲乙丙丁![]() 人中至少有
人中至少有![]() 人参加且甲乙不同时参加,丙丁也不同时参加,则不同的报名方案有( )
人参加且甲乙不同时参加,丙丁也不同时参加,则不同的报名方案有( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,点
,点![]() 的极坐标为
的极坐标为![]() ,以极点
,以极点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)曲线![]() 的直角坐标方程和点
的直角坐标方程和点![]() 的直角坐标;
的直角坐标;
(2)若过点![]() 且倾斜角为
且倾斜角为![]() 的直线
的直线![]() ,点
,点![]() 为曲线
为曲线![]() 上任意一点,求点
上任意一点,求点![]() 到直线
到直线![]() 的最小距离.
的最小距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究机构随机调查了![]() ,
,![]() 两个企业各100名员工,得到了
两个企业各100名员工,得到了![]() 企业员工月均收入的频数分布表以及
企业员工月均收入的频数分布表以及![]() 企业员工月均收入的统计图如下:
企业员工月均收入的统计图如下:
![]() 企业:
企业:
工资 | 人数 |
| 5 |
| 10 |
| 20 |
| 42 |
| 18 |
| 3 |
| 1 |
| 1 |
![]() 企业:
企业:
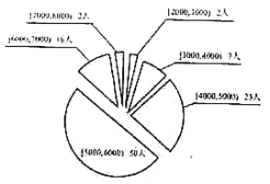
(1)若将频率视为概率,现从![]() 企业中随机抽取一名员工,求该员工月均收入不低于5000元的概率;
企业中随机抽取一名员工,求该员工月均收入不低于5000元的概率;
(2)(i)若从![]() 企业的月均收入在
企业的月均收入在![]() 员工中,按分层抽样的方式抽取7人,而后在此7人中随机抽取2人,则2人月均收入都不在
员工中,按分层抽样的方式抽取7人,而后在此7人中随机抽取2人,则2人月均收入都不在![]() 的概率是多少?
的概率是多少?
(ii)若你是一名即将就业的大学生,根据上述调查结果,并结合统计学相关知识,你会选择去哪个企业就业,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
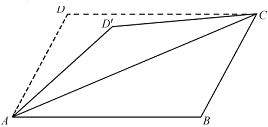
【题目】如图,四边形ABCD为矩形,沿AB将△ADC翻折成![]() .设二面角
.设二面角![]() 的平面角为
的平面角为![]() ,直线
,直线![]() 与直线BC所成角为
与直线BC所成角为![]() ,直线
,直线![]() 与平面ABC所成角为
与平面ABC所成角为![]() ,当
,当![]() 为锐角时,有
为锐角时,有
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 的展开式中第5项与第7项的二项数系数相等,且展开式的各项系数之和为1024,则下列说法正确的是( )
的展开式中第5项与第7项的二项数系数相等,且展开式的各项系数之和为1024,则下列说法正确的是( )
A.展开式中奇数项的二项式系数和为256
B.展开式中第6项的系数最大
C.展开式中存在常数项
D.展开式中含![]() 项的系数为45
项的系数为45
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我市南澳县是广东唯一的海岛县,海区面积广阔,发展太平洋牡蛎养殖业具有得天独厚的优势,所产的“南澳牡蛎”是中国国家地理标志产品,产量高、肉质肥、营养好,素有“海洋牛奶精品”的美誉.根据养殖规模与以往的养殖经验,产自某南澳牡蛎养殖基地的单个“南澳牡蛎”质量(克)在正常环境下服从正态分布![]() .
.
(1)购买10只该基地的“南澳牡蛎”,会买到质量小于20g的牡蛎的可能性有多大?
(2)2019年该基地考虑增加人工投入,现有以往的人工投入增量x(人)与年收益增量y(万元)的数据如下:
人工投入增量x(人) | 2 | 3 | 4 | 6 | 8 | 10 | 13 |
年收益增量y(万元) | 13 | 22 | 31 | 42 | 50 | 56 | 58 |
该基地为了预测人工投入增量为16人时的年收益增量,建立了y与x的两个回归模型:
模型①:由最小二乘公式可求得y与x的线性回归方程:![]() ;
;
模型②:由散点图的样本点分布,可以认为样本点集中在曲线:![]() 的附近,对人工投入增量x做变换,令
的附近,对人工投入增量x做变换,令![]() ,则
,则![]() ,且有
,且有 .
.

(i)根据所给的统计量,求模型②中y关于x的回归方程(精确到0.1);
(ii)根据下列表格中的数据,比较两种模型的相关指数![]() ,并选择拟合精度更高、更可靠的模型,预测人工投入增量为16人时的年收益增量.
,并选择拟合精度更高、更可靠的模型,预测人工投入增量为16人时的年收益增量.
回归模型 | 模型① | 模型② |
回归方程 |
|
|
| 182.4 | 79.2 |
附:若随机变量![]() ,则
,则![]() ,
,![]() ;
;
样本![]() 的最小二乘估计公式为:
的最小二乘估计公式为: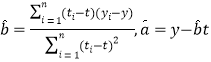 ,
,
另,刻画回归效果的相关指数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com