
【题目】“求方程 ![]() 的解”有如下解题思路:设
的解”有如下解题思路:设 ![]() ,则
,则 ![]() 在
在 ![]() 上单调递减,且
上单调递减,且 ![]() ,所以原方程有唯一解
,所以原方程有唯一解 ![]() .类比上述解题思路,不等式
.类比上述解题思路,不等式 ![]() 的解集是 .
的解集是 .
【答案】![]()
【解析】不等式x6﹣(x+2)>(x+2)3﹣x2变形为,x6+x2>(x+2)3+(x+2);
令u=x2 , v=x+2,则x6+x2>(x+2)3+(x+2)u3+u>v3+v;考察函数f(x)=x3+x,知f(x)在R上为增函数,∴f(u)>f(v),∴u>v;
不等式x6+x2>(x+2)3+(x+2)可化为x2>x+2,解得x<﹣1或x>2;∴不等式的解集为:(﹣∞,﹣1)∪(2,+∞).
故答案为:(﹣∞,﹣1)∪(2,+∞).
根据题意合理构造新的函数利用构造的新函数的单调性,把问题转化为自变量之间的关系问题再由整体思想从整体上把握结构找到结构点的相似处同一问题即可。


科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,
, ![]() .
.
(Ⅰ)当 ![]() 在
在 ![]() 处的切线与直线
处的切线与直线 ![]() 垂直时,方程
垂直时,方程 ![]() 有两相异实数根,求
有两相异实数根,求 ![]() 的取值范围;
的取值范围;
(Ⅱ)若幂函数 ![]() 的图象关于
的图象关于 ![]() 轴对称,求使不等式
轴对称,求使不等式 ![]() 在
在 ![]() 上恒成立的
上恒成立的 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代名著《庄子天下篇》中有一句名言“一尺之棰,日取其半,万世不竭”,其意思为:一尺的木棍,每天截取一半,永远都截不完,现将该木棍依此规律截取,如图所示的程序框图的功能就是计算截取7天后所剩木棍的长度(单位:尺),则①②③处可分别填入的是( )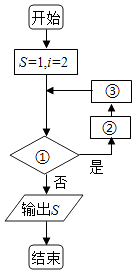
A.①i≤7?②s=s﹣ ![]() ③i=i+1
③i=i+1
B.①i≤128?②s=s﹣ ![]() ③i=2i
③i=2i
C.①i≤7?②s=s﹣ ![]() ③i=i+1
③i=i+1
D.①i≤128?②s=s﹣ ![]() ③i=2i
③i=2i
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com