
【题目】已知 ![]() ,直线
,直线 ![]() 的斜率之积为
的斜率之积为 ![]() .
.
(Ⅰ)求顶点 ![]() 的轨迹方程
的轨迹方程 ![]() ;
;
(Ⅱ)设动直线 ![]()
![]() ,点
,点 ![]() 关于直线
关于直线 ![]() 的对称点为
的对称点为 ![]() ,且
,且 ![]() 点在曲线
点在曲线 ![]() 上,求
上,求 ![]() 的取值范围.
的取值范围.
【答案】解:(Ⅰ)设动点M(x,y),则M(x,y)满足:![]()
![]() C:
C: ![]() ,
,
又 ![]() ,所以
,所以 ![]() ,
,
故答案为:M点的轨迹方程C是: ![]()
![]() .
.
(Ⅱ)由题意,设点 ![]() ,由点
,由点 ![]() 关于直线
关于直线 ![]() 的对称点为
的对称点为 ![]() ,
,
则线段 ![]() 的中点
的中点 ![]() 的坐标为
的坐标为 ![]()
![]() 且
且 ![]() .
.
又直线 ![]() 的斜率
的斜率 ![]() ,故直线
,故直线 ![]() 的斜率
的斜率 ![]() ,
,
且过点 ![]() ,所以直线
,所以直线 ![]() 的方程为:
的方程为: ![]() .
.
令 ![]() ,得
,得 ![]() ,
,
由 ![]() ,得
,得 ![]() ,
,
则 ![]() ,
, ![]() ,
,
又 ![]() ,当且仅当
,当且仅当 ![]() 时等号成立,
时等号成立,
故答案为:m的取值范围为 ![]() 或
或 ![]()
【解析】(1)设动点M的坐标为(x,y),利用斜率之积已知,结合斜率公式得到关于点M的坐标的方程即为所求.
(2)由于点PQ关于直线l对称,可将PQ中点D的坐标用点P的坐标表示出来,同时将直线l的斜率也表示出来,即将直线l的方程用点P的坐标不表示,令x=0,将m表示为点P的坐标的函数式,用均值不等式求最值.


科目:高中数学 来源: 题型:
【题目】数列{an}是以a为首项,q为公比的等比数列,数列{bn}满足bn=1+a1+a2+…+an(n=1,2,…),数列{cn}满足cn=2+b1+b2+…+bn(n=1,2,…).若{cn}为等比数列,则a+q=( )
A.![]()
B.3
C.![]()
D.6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)(x∈R)满足f(1)=1,且f(x)的导函数f′(x)< ![]() ,则f(x)<
,则f(x)< ![]() 的解集为( )
的解集为( )
A.{x|-1<x<1}
B.{x|x<-1}
C.{x|x<-1,或x>1}
D.{x|x>1}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设 ![]() 是定义在
是定义在 ![]() 上的函数,则“函数
上的函数,则“函数 ![]() 为偶函数”是“函数
为偶函数”是“函数 ![]() 为奇函数”的( )
为奇函数”的( )
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某校高中男生中随机选取100名学生,将他们的体重(单位: ![]() )数据绘制成频率分布直方图,如图所示.
)数据绘制成频率分布直方图,如图所示.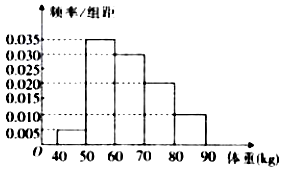
(1)估计该校的100名同学的平均体重(同一组数据以该组区间的中点值作代表);
(2)若要从体重在 ![]() ,
, ![]() ,
, ![]() 三组内的男生中,用分层抽样的方法选取6人组成一个活动队,再从这6人中选2人当正副队长,求这2人中至少有1人体重在
三组内的男生中,用分层抽样的方法选取6人组成一个活动队,再从这6人中选2人当正副队长,求这2人中至少有1人体重在 ![]() 内的概率.
内的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com