【题目】已知椭圆 
的左、右焦点分别为 
， 
，若椭圆上存在点 
使 
成立，则该椭圆的离心率的取值范围为 ．
【答案】
【解析】在△PF1F2中，由正弦定理得： 
，则由已知得： 
，
即：a|PF1|=|cPF2|
设点（x0 ， y0）由焦点半径公式，
得：|PF1|=a+ex0 ， |PF2|=a-ex0,则a（a+ex0）=c（a-ex0）
解得：x0= 
，由椭圆的几何性质知：x0＞-a则 
>-a
整理得e2+2e-1＞0，解得：e＜- 
-1或e＞ -1，又e∈（0，1），
故椭圆的离心率：e∈( -1，1).
故答案为：( -1，1)．
先用正弦定理将条件转化,为a,c与点P的焦半径间的关系,再用焦半径长公式将点P的横坐标表示为a,c的形式,用点P的横坐标的范围整理为关于a,c的齐次不等式,求离心率的范围.
科目：高中数学 来源： 题型：
【题目】设 
是定义在 
上的函数，则“函数 为偶函数”是“函数 
为奇函数”的（ ）
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】我市某小学三年级有甲、乙两个班，其中甲班有男生30人，女生20人，乙班有男生25人，女生25人，现在需要各班按男、女生分层抽取 
的学生进行某项调查，则两个班共抽取男生人数是 ．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，正方体 
的棱长为1， 
分别是棱 
的中点，过 
的平面与棱 
分别交于点 
.设 
， 
．
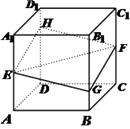
①四边形 
一定是菱形；② 
平面 ；③四边形 的面积 
在区间 
上具有单调性；④四棱锥 
的体积为定值.
以上结论正确的个数是（ ）
A.4
B.3
C.2
D.1
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在四棱锥
中，底面
为平行四边形， 
， 
， 
， 
点在底面
内的射影
在线段
上，且
， 
， 
为
的中点， 
在线段
上，且
．
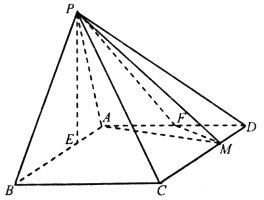
（Ⅰ）当
时，证明：平面
平面
；
（Ⅱ）当平面
与平面
所成的二面角的正弦值为
时，求四棱锥
的体积．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
