
【题目】已知抛物线![]() 的经过点
的经过点![]() .
.
(1)求抛物线的方程;
(2)过抛物线焦点F的直线l交抛物线于A、B两点,若|AB|=8,求直线l的方程.
 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:高中数学 来源: 题型:
【题目】已知圆台侧面的母线长为![]() ,母线与轴的夹角为
,母线与轴的夹角为![]() ,一个底面的半径是另一个底面半径的
,一个底面的半径是另一个底面半径的![]() 倍.
倍.

(1)求圆台两底面的半径;
(2)如图,点![]() 为下底面圆周上的点,且
为下底面圆周上的点,且![]() ,求
,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,CM,CN为某公园景观湖胖的两条木栈道,∠MCN=120°,现拟在两条木栈道的A,B处设置观景台,记BC=a,AC=b,AB=c(单位:百米)
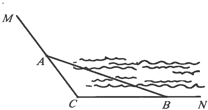
(1)若a,b,c成等差数列,且公差为4,求b的值;
(2)已知AB=12,记∠ABC=θ,试用θ表示观景路线A-C-B的长,并求观景路线A-C-B长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,从参加环保知识竞赛的1200名学生中抽出![]() 名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形,回答下列问题:
名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形,回答下列问题:

(1)![]() 这一组的频数、频率分别是多少?
这一组的频数、频率分别是多少?
(2)估计这次环保知识竞赛的及格率。(![]() 分及以上为及格)
分及以上为及格)
(3)若准备取成绩最好的300名发奖,则获奖的最低分数约为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,随着我国汽车消费水平的提高,二手车流通行业得到迅猛发展.某汽车交易市场对2017年成交的二手车交易前的使用时间(以下简称“使用时间”)进行统计,得到频率分布直方图如图1.
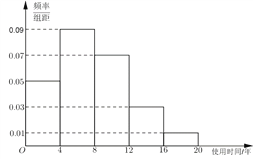

图1 图2
(1)记“在![]() 年成交的二手车中随机选取一辆,该车的使用年限在
年成交的二手车中随机选取一辆,该车的使用年限在![]() ”为事件
”为事件![]() ,试估计
,试估计![]() 的概率;
的概率;
(2)根据该汽车交易市场的历史资料,得到散点图如图2,其中![]() (单位:年)表示二手车的使用时间,
(单位:年)表示二手车的使用时间,![]() (单位:万元)表示相应的二手车的平均交易价格.由散点图看出,可采用
(单位:万元)表示相应的二手车的平均交易价格.由散点图看出,可采用![]() 作为二手车平均交易价格
作为二手车平均交易价格![]() 关于其使用年限
关于其使用年限![]() 的回归方程,相关数据如下表(表中
的回归方程,相关数据如下表(表中![]() ,
,![]() ):
):
|
|
|
|
|
|
5.5 | 8.7 | 1.9 | 301.4 | 79.75 | 385 |
①根据回归方程类型及表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
②该汽车交易市场对使用8年以内(含8年)的二手车收取成交价格![]() 的佣金,对使用时间8年以上(不含8年)的二手车收取成交价格
的佣金,对使用时间8年以上(不含8年)的二手车收取成交价格![]() 的佣金.在图1对使用时间的分组中,以各组的区间中点值代表该组的各个值.若以2017年的数据作为决策依据,计算该汽车交易市场对成交的每辆车收取的平均佣金.
的佣金.在图1对使用时间的分组中,以各组的区间中点值代表该组的各个值.若以2017年的数据作为决策依据,计算该汽车交易市场对成交的每辆车收取的平均佣金.
附注:①对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ;
;
②参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在著名的汉诺塔问题中,有三根高度相同的柱子和一些大小及颜色各不相同的圆盘,三根柱子分别为起始柱、辅助柱及目标柱.已知起始柱上套有![]() 个圆盘,较大的圆盘都在较小的圆盘下面.现把圆盘从起始柱全部移到目标柱上,规则如下:每次只能移动一个圆盘,且每次移动后,每根柱上较大的圆盘不能放在较小的圆盘上面,规定一个圆盘从任一根柱上移动到另一根柱上为一次移动.若将
个圆盘,较大的圆盘都在较小的圆盘下面.现把圆盘从起始柱全部移到目标柱上,规则如下:每次只能移动一个圆盘,且每次移动后,每根柱上较大的圆盘不能放在较小的圆盘上面,规定一个圆盘从任一根柱上移动到另一根柱上为一次移动.若将![]() 个圆盘从起始柱移动到目标柱上最少需要移动的次数记为
个圆盘从起始柱移动到目标柱上最少需要移动的次数记为![]() ,则
,则![]() ( )
( )

A. 33B. 31C. 17D. 15
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,点![]() 为圆
为圆![]() :
:![]() 上一动点,过点
上一动点,过点![]() 分别作
分别作![]() 轴,
轴,![]() 轴的垂线,垂足分别为
轴的垂线,垂足分别为![]() ,
,![]() ,连接
,连接![]() 延长至点
延长至点![]() ,使得
,使得![]() ,点
,点![]() 的轨迹记为曲线
的轨迹记为曲线![]() .
.
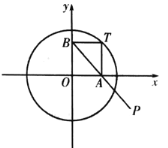
(1)求曲线![]() 的方程;
的方程;
(2)若点![]() ,
,![]() 分别位于
分别位于![]() 轴与
轴与![]() 轴的正半轴上,直线
轴的正半轴上,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,试问在曲线
两点,试问在曲线![]() 上是否存在点
上是否存在点![]() ,使得四边形
,使得四边形![]() 为平行四边形,若存在,求出直线
为平行四边形,若存在,求出直线![]() 方程;若不存在,说明理由.
方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
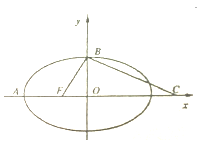
【题目】如图,F是椭圆![]() 的左焦点,椭圆的离心率为
的左焦点,椭圆的离心率为![]() ,B为椭圆的左顶点和上顶点,点C在x轴上,
,B为椭圆的左顶点和上顶点,点C在x轴上,![]() ,
,![]() 的外接圆M恰好与直线
的外接圆M恰好与直线![]() :
:![]() 相切.
相切.
![]() 1
1![]() 求椭圆的方程;
求椭圆的方程;
![]() 2
2![]() 过点C的直线
过点C的直线![]() 与已知椭圆交于P,Q两点,且
与已知椭圆交于P,Q两点,且![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com