
【题目】已知函数f(x)=x(1+m|x|),关于x的不等式f(x)>f(x+m)的解集记为T,若区间[﹣ ![]() ,
, ![]() ]T,则实数m的取值范围是( )
]T,则实数m的取值范围是( )
A.( ![]() ,0)
,0)
B.( ![]() ,0)
,0)
C.(﹣∞, ![]() )
)
D.( ![]() ,0)∪(0,
,0)∪(0, ![]() )
)
【答案】A
【解析】解:f(x)=x(1+m|x|)= ![]() ,
,
①若m=0,则不等式即f(x)>f(x ),显然不成立.
②若m>0,函数f(x)= ![]() ,在R上是增函数,如右图所示:
,在R上是增函数,如右图所示:
由f(x)>f(x+m),可得x>x+m,m<0,故m无解.
③若m<0,函数y=f(x+m)的图象是把函数y=f(x)的图象向右平移﹣m个单位得到的,
由题意可得,当x∈[﹣ ![]() ,
, ![]() ]时,函数y=f(x+m)的图象在函数 y=f(x)的图象的下方,
]时,函数y=f(x+m)的图象在函数 y=f(x)的图象的下方,
如下图所示: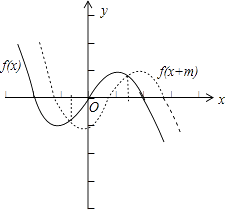
只要f(﹣ ![]() ﹣m)<f(﹣
﹣m)<f(﹣ ![]() )即可,
)即可,
即m(﹣ ![]() ﹣m)2+(﹣
﹣m)2+(﹣ ![]() ﹣m)<﹣m(﹣
﹣m)<﹣m(﹣ ![]() )2﹣
)2﹣ ![]() ,
,
即 m2﹣m﹣1<0,求得 ![]() <m<
<m< ![]() ,
,
综合可得, ![]() <m<0,
<m<0,
故选:A.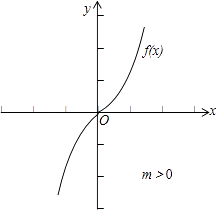


科目:高中数学 来源: 题型:
【题目】已知奇函数 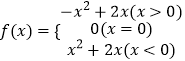
(1)在直角坐标系中画出y=f(x)的图象,并指出函数的单调区间;
(2)若函数f(x)在区间[﹣1,a﹣2]上单调递增,试确定a的取值范围. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的长半轴为
的长半轴为![]() ,短半轴为
,短半轴为![]() .椭圆
.椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() ,
,![]() ,离心率为方程
,离心率为方程![]() 的一根,长半轴为
的一根,长半轴为![]() ,短半轴为
,短半轴为![]() .若
.若![]() ,
,![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
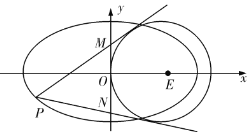
(Ⅱ)如图,过椭圆![]() 上且位于
上且位于![]() 轴左侧的一点
轴左侧的一点![]() 作圆
作圆![]()
![]() 的两条切线,分别交
的两条切线,分别交![]() 轴于点
轴于点![]() 、
、![]() .试推断是否存在点
.试推断是否存在点![]() ,使
,使![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,我艇在A处发现一走私船在方位角45°且距离为12海里的B处正以每小时10海里的速度向方位角105°的方向逃窜,我艇立即以14海里/小时的速度追击,求我艇追上走私船所需要的最短时间. 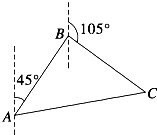
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A、B、C对应的边分别是a、b、c,C= ![]() ,且sinB=2sinAcos(A+B).
,且sinB=2sinAcos(A+B).
(1)证明:b2=2a2;
(2)若△ABC的面积是1,求边c.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=kx+log9(9x+1)(k∈R)是偶函数.
(1)求k的值;
(2)若函数g(x)=log9(a3x﹣ ![]() a)的图象与f(x)的图象有且只有一个公共点,求a的取值范围.
a)的图象与f(x)的图象有且只有一个公共点,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】双流中学2016年高中毕业的大一学生假期参加社会实践活动,为提高某套丛书的销量,准备举办一场展销会,据市场调查,当每套丛书售价定为![]() 元时,销售量可达到
元时,销售量可达到![]() 万套,现出版社为配合该书商的活动,决定进行价格改革,将每套丛书的供货价格分成固定价格和浮动价格两部分,其中固定价格为30元,浮动价格(单位:元)与销售量(单位:万套)成反比,比例系数为10,假设不计其他成本,即销售每套丛书的利润=售价
万套,现出版社为配合该书商的活动,决定进行价格改革,将每套丛书的供货价格分成固定价格和浮动价格两部分,其中固定价格为30元,浮动价格(单位:元)与销售量(单位:万套)成反比,比例系数为10,假设不计其他成本,即销售每套丛书的利润=售价![]() 供货价格.问:
供货价格.问:
(1)每套丛书售价定为100元时,书商所获得的总利润是多少万元?
(2)每套丛书售价定为多少元时,单套丛书的利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且满足 ![]() acosC﹣csinA=0.
acosC﹣csinA=0.
(1)求角C的大小;
(2)已知b=4,△ABC的面积为6 ![]() ,求边长c的值.
,求边长c的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com