
【题目】已知椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,椭圆的四个顶点围成的四边形的面积为4.
,椭圆的四个顶点围成的四边形的面积为4.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点,
两点, ![]() 的中点
的中点![]() 在圆
在圆![]() 上,求
上,求![]() (
(![]() 为坐标原点)面积的最大值.
为坐标原点)面积的最大值.
【答案】(Ⅰ)![]() .
.
(Ⅱ)1.
【解析】试题分析:(Ⅰ)由题意知, ![]() ,得
,得![]() ,
, ![]() ,代入椭圆的方程,再由椭圆
,代入椭圆的方程,再由椭圆![]() 的四个顶点围成的四边形的面积得
的四个顶点围成的四边形的面积得![]() ,求得
,求得![]() 的值,即可得到椭圆的方程;
的值,即可得到椭圆的方程;
(Ⅱ)当直线![]() 的斜率不存在时,得到
的斜率不存在时,得到![]() ,
,
当直线![]() 的斜率存在时,设
的斜率存在时,设![]() :
: ![]() ,联立方程组,求得
,联立方程组,求得![]() ,求得
,求得![]() 中点的坐标,代入圆的方程,得
中点的坐标,代入圆的方程,得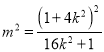 ,再由弦长公式和点到直线的距离公式,即可得到
,再由弦长公式和点到直线的距离公式,即可得到![]() 的表达式,即可求解面积的最大值.
的表达式,即可求解面积的最大值.
试题解析:
(Ⅰ)由题意知![]() ,得
,得![]() ,
, ![]() ,
,
所以![]() ,
,
由椭圆![]() 的四个顶点围成的四边形的面积为4,得
的四个顶点围成的四边形的面积为4,得![]() ,
,
所以![]() ,
, ![]() ,椭圆
,椭圆![]() 的标准方程为
的标准方程为![]() .
.
(Ⅱ)当直线![]() 的斜率不存在时,
的斜率不存在时,
令![]() ,得
,得![]() ,
, ![]() ,
,
当直线![]() 的斜率存在时,设
的斜率存在时,设![]() :
: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
由![]() ,得
,得![]() ,
,
则![]() ,
, ![]() ,
,
所以![]() ,
, ![]() ,
,
将![]() 代入
代入![]() ,得
,得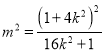 ,
,
又因为![]()
![]() ,
,
原点到直线![]() 的距离
的距离![]() ,
,
所以![]()
![]()
![]()
![]()
![]()
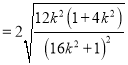
![]()
![]() .
.
当且仅当![]() ,即
,即![]() 时取等号.
时取等号.
综上所述, ![]() 面积的最大值为1.
面积的最大值为1.


科目:高中数学 来源: 题型:
【题目】用合适的方法表示下列集合,并说明是有限集还是无限集.
(1)到A、B两点距离相等的点的集合
(2)满足不等式![]() 的
的![]() 的集合
的集合
(3)全体偶数
(4)被5除余1的数
(5)20以内的质数
(6)![]()
(7)方程![]() 的解集
的解集
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,以坐标原点
,以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,直线
轴正半轴为极轴,建立极坐标系,直线![]() 的参数方程为
的参数方程为![]() (t为参数).
(t为参数).
(1)写出曲线![]() 的参数方程和直线
的参数方程和直线![]() 的普通方程;
的普通方程;
(2)已知点![]() 是曲线
是曲线![]() 上一点,,求点
上一点,,求点![]() 到直线
到直线![]() 的最小距离.
的最小距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为原点,以极轴为
,以极点为原点,以极轴为![]() 轴的正半轴,取相同的单位长度,建立平面直角坐标系,直线
轴的正半轴,取相同的单位长度,建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为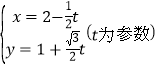 .
.
(1)写出直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设曲线![]() 经过伸缩变换
经过伸缩变换![]() 得到曲线
得到曲线![]() ,曲线
,曲线![]() 上任一点为
上任一点为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从2017年1月18日开始,支付宝用户可以通过“![]() 扫‘福’字”和“参与蚂蚁森林”两种方式获得福卡(爱国福、富强福、和谐福、友善福,敬业福),除夕夜22:18,每一位提前集齐五福的用户都将获得一份现金红包.某高校一个社团在年后开学后随机调查了80位该校在读大学生,就除夕夜22:18之前是否集齐五福进行了一次调查(若未参与集五福的活动,则也等同于未集齐五福),得到具体数据如下表:
扫‘福’字”和“参与蚂蚁森林”两种方式获得福卡(爱国福、富强福、和谐福、友善福,敬业福),除夕夜22:18,每一位提前集齐五福的用户都将获得一份现金红包.某高校一个社团在年后开学后随机调查了80位该校在读大学生,就除夕夜22:18之前是否集齐五福进行了一次调查(若未参与集五福的活动,则也等同于未集齐五福),得到具体数据如下表:
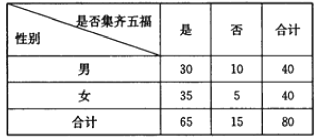
(1)根据如上的列联表,能否在犯错误的概率不超过0.05的前提下,认为“集齐五福与性别有关”?
(2)计算这80位大学生集齐五福的频率,并据此估算该校10000名在读大学生中集齐五福的人数;
(3)为了解集齐五福的大学生明年是否愿意继续参加集五福活动,该大学的学生会从集齐五福的学生中,选取2位男生和3位女生逐个进行采访,最后再随机选取3次采访记录放到该大学的官方网站上,求最后被选取的3次采访对象中至少有一位男生的概率.
参考公式: 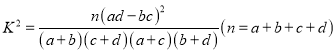 .
.
附表:

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,函数
,函数![]() .
.
⑴若![]() 的定义域为
的定义域为![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
⑵当![]() ,求函数
,求函数![]() 的最小值
的最小值![]() ;
;
⑶是否存在实数![]() ,使得函数
,使得函数![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,则说明理由.
的值;若不存在,则说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在梯形![]() 中(图1),
中(图1),![]() ,
, ![]() ,
, ![]() ,过
,过![]() 、
、![]() 分别作
分别作![]() 的垂线,垂足分别为
的垂线,垂足分别为![]() 、
、![]() ,已知
,已知![]() ,
, ![]() ,将梯形
,将梯形![]() 沿
沿![]() 、
、![]() 同侧折起,使得
同侧折起,使得![]() ,
, ![]() ,得空间几何体
,得空间几何体![]() (图2).
(图2).
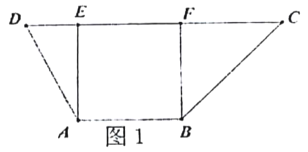
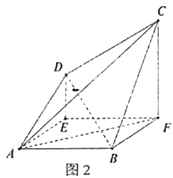
(1)证明: ![]() 平面
平面![]() ;
;
(2)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】底面为菱形且侧棱垂直于底面的四棱柱![]() 中,
中, ![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 的中点,过点
的中点,过点![]() ,
, ![]() ,
, ![]() ,
, ![]() 的平面截直四棱柱
的平面截直四棱柱![]() ,得到平面四边形
,得到平面四边形![]() ,
, ![]() 为
为![]() 的中点,且
的中点,且![]() ,当截面的面积取最大值时,
,当截面的面积取最大值时, ![]() 的值为( )
的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() 所对的边分别为
所对的边分别为![]() ,
,![]() ,
,![]() ,过
,过![]() 作直线
作直线![]() 与边
与边![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() .当直线
.当直线![]() 时,
时,![]() 值为
值为![]() ;当
;当![]() 为边
为边![]() 的中点时,
的中点时,![]() 值为
值为![]() .当
.当![]() ,
,![]() 变化时,记
变化时,记![]() (即
(即![]() 、
、![]() 中较大的数),则
中较大的数),则![]() 的最小值为( )
的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.1
D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com