
【题目】已知函数![]() .
.
(Ⅰ)求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)证明:函数![]() 在区间
在区间![]() 上存在唯一的极大值点;
上存在唯一的极大值点;
(Ⅲ)证明:函数![]() 有且仅有一个零点.
有且仅有一个零点.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】随着电商的快速发展,快递业突飞猛进,到目前,中国拥有世界上最大的快递市场.某快递公司收取快递费用的标准是:重量不超过![]() 的包裹收费10元;重量超过
的包裹收费10元;重量超过![]() 的包裹,除
的包裹,除![]() 收费10元之外,每超过
收费10元之外,每超过![]() (不足
(不足![]() ,按
,按![]() 计算)需再收5元.
计算)需再收5元.
该公司将最近承揽的100件包裹的重量统计如下:
包裹重量(单位: | 1 | 2 | 3 | 4 | 5 |
包裹件数 | 43 | 30 | 15 | 8 | 4 |
公司对近60天,每天揽件数量统计如下表:
包裹件数范围 | 0~100 | 101~200 | 201~300 | 301~400 | 401~500 |
包裹件数(近似处理) | 50 | 150 | 250 | 350 | 450 |
天数 | 6 | 6 | 30 | 12 | 6 |
以上数据已做近似处理,并将频率视为概率.
(1)计算该公司未来5天内恰有2天揽件数在101~300之间的概率;
(2)①估计该公司对每件包裹收取的快递费的平均值;
②根据以往的经验,公司将快递费的三分之一作为前台工作人员的工资和公司利润,剩余的用作其他费用.目前前台有工作人员3人,每人每件揽件不超过150件,日工资100元.公司正在考虑是否将前台工作人员裁减1人,试计算裁员前后公司每日利润的数学期望,若你是公司老总,是否进行裁减工作人员1人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为坐标原点,点
为坐标原点,点![]() ,
,![]() ,
,![]() ,动点
,动点![]() 满足
满足![]() ,点
,点![]() 为线段
为线段![]() 的中点,抛物线
的中点,抛物线![]() :
:![]() 上点
上点![]() 的纵坐标为
的纵坐标为![]() ,
,![]() .
.
(1)求动点![]() 的轨迹曲线
的轨迹曲线![]() 的标准方程及抛物线
的标准方程及抛物线![]() 的标准方程;
的标准方程;
(2)若抛物线![]() 的准线上一点
的准线上一点![]() 满足
满足![]() ,试判断
,试判断![]() 是否为定值,若是,求这个定值;若不是,请说明理由.
是否为定值,若是,求这个定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
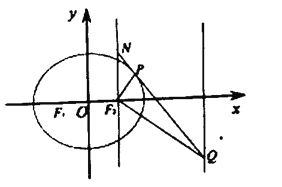
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() ,椭圆
,椭圆![]() 上一点
上一点![]() 到
到![]() 的距离之和为4.过点
的距离之和为4.过点![]() 作直线
作直线![]() 的垂线
的垂线![]() 交直线
交直线![]() 于点
于点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)试判断直线![]() 与椭圆
与椭圆![]() 公共点的个数,并说明理由;
公共点的个数,并说明理由;
(3)直线![]() 与直线
与直线![]() 交于点
交于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】斜率为![]() 的直线
的直线![]() 过抛物线
过抛物线![]() 的焦点
的焦点![]() ,且与抛物线
,且与抛物线![]() 交于
交于![]() 、
、![]() 两点.
两点.
(1)设点![]() 在第一象限,过
在第一象限,过![]() 作抛物线
作抛物线![]() 的准线的垂线,
的准线的垂线,![]() 为垂足,且
为垂足,且![]() ,直线
,直线![]() 与直线
与直线![]() 关于直线
关于直线![]() 对称,求直线
对称,求直线![]() 的方程;
的方程;
(2)过![]() 且与
且与![]() 垂直的直线
垂直的直线![]() 与圆
与圆![]() 交于
交于![]() 、
、![]() 两点,若
两点,若![]() 与
与![]() 面积之和为
面积之和为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (其中
(其中![]() 为自然对数的底数).
为自然对数的底数).
(1)若![]() ,求函数
,求函数![]() 在区间
在区间![]() 上的最大值;
上的最大值;
(2)若![]() ,关于
,关于![]() 的方程
的方程![]() 有且仅有一个根, 求实数
有且仅有一个根, 求实数![]() 的取值范围;
的取值范围;
(3)若对任意![]() ,不等式
,不等式![]() 均成立, 求实数
均成立, 求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com