
【题目】已知![]() 分别为椭圆
分别为椭圆![]() 的上、下焦点,
的上、下焦点,![]() 是抛物线
是抛物线![]() 的焦点,点
的焦点,点![]() 是
是![]() 与
与![]() 在第二象限的交点,且
在第二象限的交点,且![]() .
.

(1)求椭圆![]() 的方程;
的方程;
(2)与圆![]() 相切的直线
相切的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,若椭圆
,若椭圆![]() 上一点
上一点![]() 满足
满足![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() 且
且![]() ,且
,且![]() .
.
【解析】
试题分析:(1)利用抛物线的方程和定义,即可求出点![]() 的坐标,再利用椭圆的定义即可求出椭圆
的坐标,再利用椭圆的定义即可求出椭圆![]() 的方程;(2)根据直线与圆相切,则圆心到直线的距离定于半径,可得
的方程;(2)根据直线与圆相切,则圆心到直线的距离定于半径,可得![]() ,联立直线与椭圆方程,结合椭圆上一点
,联立直线与椭圆方程,结合椭圆上一点![]() 满足
满足![]() ,可得
,可得![]() 的表达式,进而求出实数
的表达式,进而求出实数![]() 的取值范围.
的取值范围.
试题解析:(1)由题知![]() ,所以
,所以![]() ,
,
又由抛物线定义可知![]() ,得
,得![]() ,
,
于是易知![]() ,从而
,从而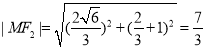 ,
,
由椭圆定义知![]() ,得
,得![]() ,故
,故![]() ,
,
从而椭圆的方程为![]() .
.
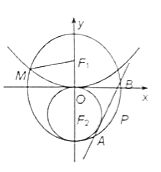
(2)设![]() ,
,![]() ,
,![]() ,则由知
,则由知![]() ,
,
![]() ,
,![]() ,且
,且![]() ,………………①
,………………①
又直线![]() 与圆
与圆![]() 相切,所以有
相切,所以有![]() ,
,
由![]() ,可得
,可得![]() ,………………②
,………………②
又联立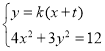 ,消去
,消去![]() 得
得![]() .
.
且![]() 恒成立,且
恒成立,且![]() ,
,![]() ,
,
所以![]() ,所以得
,所以得![]()
代入①式得![]() ,所以
,所以![]() ,
,
又将②式代入得,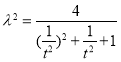 ,
,![]() ,
,![]() ,
,
易知![]() ,且
,且![]() ,所以
,所以![]() .
.
所以![]() 的取值范围为
的取值范围为![]() 且
且![]() ,且
,且![]()


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:
【题目】已知直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,且线段
两点,且线段![]() 恰好被点
恰好被点![]() 平分.
平分.
(1)求直线![]() 的方程;
的方程;
(2)抛物线上是否存在点![]() 和
和![]() ,使得
,使得![]() 关于直线
关于直线![]() 对称?若存在,求出直线
对称?若存在,求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知α、β是不同的平面,l、m、n是不同的直线,P为空间中一点.若α∩β=l,mα、nβ、m∩n=P,则点P与直线l的位置关系用符号表示为___.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 定义在区间
定义在区间![]() 内,对于任意的
内,对于任意的![]() ,有
,有![]() ,且当
,且当![]() 时,
时,![]() .
.
(1)验证函数![]() 是否满足这些条件;
是否满足这些条件;
(2)判断这样的函数是否具有奇偶性和单调性,并加以证明;
(3)若![]() ,求方程
,求方程![]() 的解.
的解.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面是一个2×2列联表,则表中a、b的值分别为 ( )
y1 | y2 | 合计 | |
x1 | a | 21 | 73 |
x2 | 2 | 25 | 27 |
合计 | b | 46 | 100 |
A. 94、96 B. 52、50
C. 52、54 D. 54、52
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com