
 连线的斜率之积为1,点C的坐标为(1,0).
连线的斜率之积为1,点C的坐标为(1,0). 为常数.
为常数. 与
与 ,(x
,(x ),由题设知
),由题设知 ,由此能求出点P的轨迹方程.
,由此能求出点P的轨迹方程. ,由此能求出
,由此能求出 =-1.直线斜率不存在时,E(2,
=-1.直线斜率不存在时,E(2, ),F(2,-
),F(2,- ),
), .所以
.所以 为常数-1.
为常数-1. 与
与 ,(x
,(x ),…(2分)
),…(2分) 连线的斜率之积为1,
连线的斜率之积为1, ,
, ).…(5分)
).…(5分) ,…(8分)
,…(8分)

 -(1+2k2)•
-(1+2k2)• +1+4k2
+1+4k2 ,解得E(2,
,解得E(2, ),F(2,-
),F(2,- ),
), =-1. …(12分)
=-1. …(12分) .
. 为常数-1.…(12分)
为常数-1.…(12分)

 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:
| 2 |
| 2 |
| CE |
| CF |
查看答案和解析>>
科目:高中数学 来源:模拟题 题型:解答题
 ,0),B(
,0),B(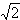 ,0)连线的斜率之积为1,点C的坐标为(1,0)。
,0)连线的斜率之积为1,点C的坐标为(1,0)。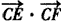 为常数。
为常数。查看答案和解析>>
科目:高中数学 来源:武昌区模拟 题型:解答题
| 2 |
| 2 |
| CE |
| CF |
查看答案和解析>>
科目:高中数学 来源:0117 期末题 题型:解答题
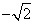 ,0),B(
,0),B(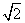 ,0)连线的斜率之积为1,点C的坐标为(1,0),
,0)连线的斜率之积为1,点C的坐标为(1,0),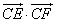 为常数。
为常数。 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com