
【题目】如图,在Rt△ABC中,∠C=90°,D,E分别为AC,AB的中点,点F为线段CD上的一点.将△ADE沿DE折起到△A1DE的位置,使A1F⊥CD,如图2.
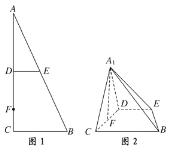
(1)求证:DE∥平面A1CB;
(2)求证:A1F⊥BE;
(3)线段A1B上是否存在点Q,使A1C⊥平面DEQ?说明理由.
【答案】(1)详见解析(2)详见解析(3)线段A1B上存在点Q,使得A1C⊥平面DEQ
【解析】
试题分析:(1)D,E分别为AC,AB的中点,易证DE∥平面A1CB;(2)由题意可证DE⊥平面A1DC,从而有DE⊥A1F,又A1F⊥CD,可证A1F⊥平面BCDE,问题解决;(3)取A1C,A1B的中点P,Q,则PQ∥BC,平面DEQ即为平面DEP,由DE⊥平面,P是等腰三角形DA1C底边A1C的中点,可证A1C⊥平面DEP,从而A1C⊥平面DEQ
试题解析:(1)证明:因为D,E分别为AC,AB的中点,
所以DE∥BC.
又因为DE平面A1CB,
所以DE∥平面A1CB.
(2)证明:由已知得AC⊥BC且DE∥BC,
所以DE⊥AC.
所以DE⊥A1D,DE⊥CD.所以DE⊥平面A1DC.
而A1F平面A1DC,所以DE⊥A1F.
又因为A1F⊥CD,
所以A1F⊥平面BCDE.所以A1F⊥BE.
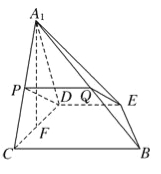
(3)线段A1B上存在点Q,使A1C⊥平面DEQ.理由如下:
如图,分别取A1C,A1B的中点P,Q,则PQ∥BC.
又因为DE∥BC,所以DE∥PQ.
所以平面DEQ即为平面DEP.
由(2)知,DE⊥平面A1DC,所以DE⊥A1C.
又因为P是等腰三角形DA1C底边A1C的中点,
所以A1C⊥DP.所以A1C⊥平面DEP.从而A1C⊥平面DEQ.
故线段A1B上存在点Q,使得A1C⊥平面DEQ.


科目:高中数学 来源: 题型:
【题目】如下图,已知四棱锥![]() 中,底面
中,底面![]() 为菱形,
为菱形,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点.
的中点.

(I)证明:![]() 平面
平面![]() ;
;
(II)取![]() ,在线段
,在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 与平面
与平面![]() 所成最大角的正切值为
所成最大角的正切值为![]() ,若存在,请求出
,若存在,请求出![]() 点的位置;若不存在,请说明理由.
点的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某飞机失联,经卫星侦查,其最后出现在小岛![]() 附近,现派出四艘搜救船
附近,现派出四艘搜救船![]() ,为方便联络,船
,为方便联络,船![]() 始终在以小岛
始终在以小岛![]() 为圆心,100海里为半径的圆上,船
为圆心,100海里为半径的圆上,船![]() 构成正方形编队展开搜索,小岛
构成正方形编队展开搜索,小岛![]() 在正方形编队外(如图).设小岛
在正方形编队外(如图).设小岛![]() 到
到![]() 的距离为
的距离为![]() ,
,![]() ,
,![]() 船到小岛
船到小岛![]() 的距离为
的距离为![]() .
.
(1)请分别求![]() 关于
关于![]() 的函数关系式
的函数关系式![]() ,并分别写出定义域;
,并分别写出定义域;
(2)当![]() 两艘船之间的距离是多少时搜救范围最大(即
两艘船之间的距离是多少时搜救范围最大(即![]() 最大)?
最大)?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,
(1)当![]() 时,证明:函数
时,证明:函数![]() 不是奇函数;
不是奇函数;
(2)判断函数![]() 的单调性,并利用函数单调性的定义给出证明;
的单调性,并利用函数单调性的定义给出证明;
(3)若![]() 是奇函数,且
是奇函数,且![]() 在
在![]() 时恒成立,求实数
时恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
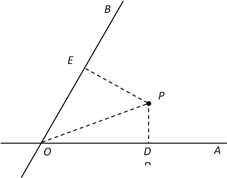
【题目】如图,![]() 、
、![]() 是两条公路(近似看成两条直线),
是两条公路(近似看成两条直线),![]() ,在
,在![]() 内有一纪念塔
内有一纪念塔![]() (大小忽略不计),已知
(大小忽略不计),已知![]() 到直线
到直线![]() 、
、![]() 的距离分别为
的距离分别为![]() 、
、![]() ,
,![]() =6千米,
=6千米,![]() =12千米.现经过纪念塔
=12千米.现经过纪念塔![]() 修建一条直线型小路,与两条公路
修建一条直线型小路,与两条公路![]() 、
、![]() 分别交于点
分别交于点![]() 、
、![]() .
.
(1)求纪念塔![]() 到两条公路交点
到两条公路交点![]() 处的距离;
处的距离;
(2)若纪念塔![]() 为小路
为小路![]() 的中点,求小路
的中点,求小路![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,点
,点![]() 也为抛物线
也为抛物线![]() 的焦点,过点
的焦点,过点![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于
于![]() 两点.
两点.
(Ⅰ)若点![]() 满足
满足![]() ,求直线
,求直线![]() 的方程;
的方程;
(Ⅱ)![]() 为直线
为直线![]() 上任意一点,过点
上任意一点,过点![]() 作
作![]() 的垂线交椭圆
的垂线交椭圆![]() 于
于![]() 两点,求
两点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市![]() 户居民的月平均用电量(单位:度),以
户居民的月平均用电量(单位:度),以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分组的频率分布直方图如图.
分组的频率分布直方图如图.
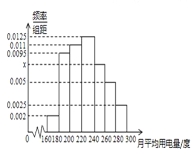
(I)求直方图中![]() 的值;
的值;
(II)求月平均用电量的众数和中位数;
(III)在月平均用电量为![]() ,
,![]() ,
,![]() ,
,![]() 的四组用户中,用分层抽样的方法抽取
的四组用户中,用分层抽样的方法抽取![]() 户居民,则月平均用电量在
户居民,则月平均用电量在![]() 的用户中应抽取多少户?
的用户中应抽取多少户?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com