
【题目】已知函数![]() ,
,
(1)当![]() 时,证明:函数
时,证明:函数![]() 不是奇函数;
不是奇函数;
(2)判断函数![]() 的单调性,并利用函数单调性的定义给出证明;
的单调性,并利用函数单调性的定义给出证明;
(3)若![]() 是奇函数,且
是奇函数,且![]() 在
在![]() 时恒成立,求实数
时恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)当![]() 时,
时,![]() ,因为
,因为![]() ,
,![]() ,
,
所以![]() ,故
,故![]() 不是奇函数; ……………………………………4分
不是奇函数; ……………………………………4分
(Ⅱ)函数![]() 在
在![]() 上为单调增函数, ………………………………………… 6分
上为单调增函数, ………………………………………… 6分
证明:设![]() ,则
,则![]() ……… 8分
……… 8分
∵![]() ,∴
,∴![]() ,
,![]() ,且
,且![]()
又∵![]() ,∴
,∴![]()
∴![]() ,故
,故![]() 。
。
∴函数![]() 在
在![]() 上为单调增函数。…………………………………………………10分
上为单调增函数。…………………………………………………10分
(Ⅲ)因为![]() 是奇函数,所以
是奇函数,所以![]() 对任意
对任意![]() 恒成立。
恒成立。
即![]() 对任意
对任意![]() 恒成立.
恒成立.
化简整理得![]() 对任意
对任意![]() 恒成立. ∴
恒成立. ∴![]() …………………12分
…………………12分
又因为![]() 在
在![]() 时恒成立,
时恒成立,
所以![]() 在
在![]() 时恒成立,
时恒成立,
令![]() ,设
,设![]() ,且
,且![]() ,
,
则![]()
由(Ⅱ)可知,![]() ,又
,又![]() ,
,
所以![]() ,即
,即![]() ,
,
故函数![]() 在
在![]() 上是增函数。………………………14分
上是增函数。………………………14分
所以![]() ,由
,由![]()
![]() 。
。
因此![]() 的取值范围是
的取值范围是![]() 。 ………………………………………………16分
。 ………………………………………………16分
【解析】试题分析:(1)举个反例,使得f(-a)≠-f(a)即可;(2)利用函数的单调性进行证明即可,注意指数函数y=2x性质的运用;(3)先根据题意求出a的值,然后f(x)≥x2-4x+m在x∈[-2,2]时恒成立,将式子变形为f(x)-(x2-4x)≥m在x∈[-2,2]时恒成立即可,在研究左边函数的单调性,求出其最小值即可
试题解析:(1)当![]() 时,
时,![]() ,因为
,因为![]() ,
,![]() ,
,
所以![]() ,故
,故![]() 不是奇函数;
不是奇函数;
(2)函数![]() 在
在![]() 上为单调增函数,
上为单调增函数,
证明:设![]() ,则
,则![]()
∵![]() ,∴
,∴![]() ,
,![]() ,且
,且![]()
又∵![]() ,∴
,∴![]()
∴![]() ,故
,故![]()
∴函数![]() 在
在![]() 上为单调增函数
上为单调增函数
(3)因为![]() 是奇函数,所以
是奇函数,所以![]() 对任意
对任意![]() 恒成立。
恒成立。
即![]() 对任意
对任意![]() 恒成立.
恒成立.
化简整理得![]() 对任意
对任意![]() 恒成立. ∴
恒成立. ∴![]()
因为![]() 在
在![]() 时恒成立,
时恒成立,
令![]() ,设
,设![]() ,且
,且![]() ,
,
则![]()
由(2)可知,![]() ,又
,又![]() ,
,
所以![]() ,即
,即![]() ,
,
故函数![]() 在
在![]() 上是增函数 (直接判断出单调性也给分)
上是增函数 (直接判断出单调性也给分)
所以![]() ,由
,由![]()
![]()
因此![]() 的取值范围是
的取值范围是![]()


科目:高中数学 来源: 题型:
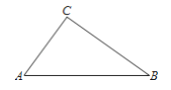
【题目】如图,A,B,C三地有直道相通,AB=5千米,AC=3千米,BC=4千米.现甲、乙两警员同时从A地出发匀速前往B地,经过t小时,他们之间的距离为![]() (单位:千米).甲的路线是AB,速度是5千米/小时,乙的路线是ACB,速度是8千米/小时,乙到达B地后原地等待,设
(单位:千米).甲的路线是AB,速度是5千米/小时,乙的路线是ACB,速度是8千米/小时,乙到达B地后原地等待,设![]() 时,乙到达C地.
时,乙到达C地.
(1)求![]() 与
与![]() 的值;
的值;
(2)已知警员的对讲机的有效通话距离是3千米.当![]() 时,求
时,求![]() 的表达式,并判断
的表达式,并判断![]() 在
在![]() 上的最大值是否超过3?并说明理由.
上的最大值是否超过3?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图, ![]() 是边长为3的正方形,
是边长为3的正方形, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
, ![]() .
.

(1)证明:平面![]() 平面
平面![]() ;
;
(2)在![]() 上是否存在一点
上是否存在一点![]() ,使平面
,使平面![]() 将几何体
将几何体![]() 分成上下两部分的体积比为
分成上下两部分的体积比为![]() ?若存在,求出点
?若存在,求出点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在
在![]() 上为增函数,且
上为增函数,且![]() ,
,![]() 为常数,
为常数, ![]() .
.
(1)求![]() 的值;(2)若
的值;(2)若![]() 在
在![]() 上为单调函数,求
上为单调函数,求![]() 的取值范围;
的取值范围;
(3)设![]() ,若在
,若在![]() 上至少存在一个
上至少存在一个![]() ,使得
,使得![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
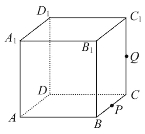
【题目】如图,正方体![]() 的棱长为1,P为BC的中点,Q为线段
的棱长为1,P为BC的中点,Q为线段![]() 上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是_________(写出所有正确命题的编号)。
上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是_________(写出所有正确命题的编号)。
①当![]() 时,S为四边形
时,S为四边形
②当![]() 时,S为等腰梯形
时,S为等腰梯形
③当![]() 时,S与
时,S与![]() 的交点R满足
的交点R满足![]()
④当![]() 时,S为六边形
时,S为六边形
⑤当![]() 时,S的面积为
时,S的面积为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,D,E分别为AC,AB的中点,点F为线段CD上的一点.将△ADE沿DE折起到△A1DE的位置,使A1F⊥CD,如图2.
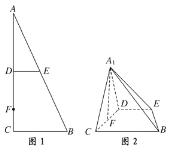
(1)求证:DE∥平面A1CB;
(2)求证:A1F⊥BE;
(3)线段A1B上是否存在点Q,使A1C⊥平面DEQ?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知平行四边形ABCD中,BC=6,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点.
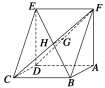
(1)求证:GH∥平面CDE;
(2)若CD=2,DB=4![]() ,求四棱锥F—ABCD的体积.
,求四棱锥F—ABCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() (
(![]() ).
).
(1)证明:直线![]() 过定点;
过定点;
(2)若直线不经过第四象限,求![]() 的取值范围;
的取值范围;
(3)若直线![]() 轴负半轴于
轴负半轴于![]() ,交
,交![]() 轴正半轴于
轴正半轴于![]() ,△
,△![]() 的面积为
的面积为![]() (
(![]() 为坐标原点),求
为坐标原点),求![]() 的最小值,并求此时直线
的最小值,并求此时直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com