
【题目】已知![]() 为坐标原点,
为坐标原点,![]() 为坐标平面内动点,且
为坐标平面内动点,且![]() 成等差数列.
成等差数列.
(1)求动点![]() 的轨迹方程;
的轨迹方程;
(2)设点![]() 的轨迹为曲线
的轨迹为曲线![]() ,过点
,过点![]() 作直线交
作直线交![]() 于
于![]() 两点(不与原点重合),是否存在
两点(不与原点重合),是否存在![]() 轴上一定点
轴上一定点![]() ,使得_________.若存在,求出定点
,使得_________.若存在,求出定点![]() ,若不存在,说明理由.从“①作
,若不存在,说明理由.从“①作![]() 点关于
点关于![]() 轴的对称点
轴的对称点![]() ,则
,则![]() 三点共线;②
三点共线;②![]() ”这两个条件中选一个,补充在上面的问题中并作答(注:如果选择两个条件分别作答,按第一个解答计分)
”这两个条件中选一个,补充在上面的问题中并作答(注:如果选择两个条件分别作答,按第一个解答计分)
【答案】(1)![]() ;(2)两种选择都存在
;(2)两种选择都存在![]() 满足条件.
满足条件.
【解析】
(1)设![]() ,
,![]() ,
,![]() ,由已知得关于
,由已知得关于![]() ,
,![]() 的关系式,整理即可求得点
的关系式,整理即可求得点![]() 的轨迹方程;
的轨迹方程;
(2)当选①时,设![]() ,与
,与![]() 联立,得关于
联立,得关于![]() 的一元二次方程,利用根与系数的关系可得
的一元二次方程,利用根与系数的关系可得![]() ,
,![]() 横坐标的和与积,写出直线
横坐标的和与积,写出直线![]() 的方程,由直线系方程可得,直线
的方程,由直线系方程可得,直线![]() 过定点
过定点![]() ,说明结论成立;
,说明结论成立;
当选②时,假设存在![]() 满足条件②,设
满足条件②,设![]() ,与
,与![]() 联立,得关于
联立,得关于![]() 的一元二次方程,利用根与系数的关系可得
的一元二次方程,利用根与系数的关系可得![]() ,
,![]() 横坐标的和与积,由
横坐标的和与积,由![]() 求得
求得![]() ,说明存在
,说明存在![]() 满足条件.
满足条件.
解:(1)设![]() ,
,![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,
由2,![]() ,
,![]() 成等差数列,得
成等差数列,得![]() ,即
,即![]() ,
,
即![]() ,化简得
,化简得![]() ,
,
![]() 点
点![]() 的轨迹方程为
的轨迹方程为![]() ;
;
(2)当选①时,设![]() ,与
,与![]() 联立,得
联立,得![]() ,
,
设![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
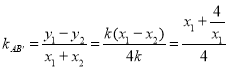 ,
,
![]() ,化简得
,化简得![]() ,
,
![]() 存在
存在![]() 满足条件.
满足条件.
当选②时,假设存在![]() 满足条件②,
满足条件②,
设![]() ,与
,与![]() 联立,得
联立,得![]() ,
,
设![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]()
![]() ,
,
![]() ,即
,即![]() ,
,
![]() 存在
存在![]() 满足条件.
满足条件.


 阶梯计算系列答案
阶梯计算系列答案科目:高中数学 来源: 题型:
【题目】某水果批发商经销某种水果(以下简称A水果),购入价为300元/袋,并以360元/袋的价格售出,若前8小时内所购进的A水果没有售完,则批发商将没售完的A水果以220元/袋的价格低价处理完毕(根据经验,2小时内完全能够把A水果低价处理完,且当天不再购进).该水果批发商根据往年的销量,统计了100天A水果在每天的前8小时内的销售量,制成如下频数分布条形图.
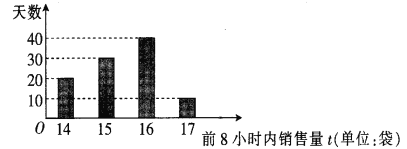
现以记录的100天的A水果在每天的前8小时内的销售量的频率作为A水果在一天的前8小时内的销售量的概率,记X表示A水果一天前8小时内的销售量,n表示水果批发商一天批发A水果的袋数.
(1)求X的分布列;
(2)以日利润的期望值为决策依据,在![]() 与
与![]() 中选其一,应选用哪个?
中选其一,应选用哪个?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线C的方程为
中,曲线C的方程为![]() ,以原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
,以原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为![]() .
.
(1)求直线l的直角坐标方程;
(2)已知P是曲线C上的一动点,过点P作直线![]() 交直线于点A,且直线
交直线于点A,且直线![]() 与直线l的夹角为45°,若
与直线l的夹角为45°,若![]() 的最大值为6,求a的值.
的最大值为6,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三棱锥P﹣ABC中.AB⊥BC,△PAC为等边三角形,二面角P﹣AC﹣B的余弦值为![]() ,当三棱锥的体积最大时,其外接球的表面积为8π.则三棱锥体积的最大值为( )
,当三棱锥的体积最大时,其外接球的表面积为8π.则三棱锥体积的最大值为( )
A.1B.2C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,函数
,函数![]()
(1)若![]() 在
在![]() 上单调递增,则
上单调递增,则![]() 的取值范围为______________;
的取值范围为______________;
(2)若对于任意实数![]() ,方程
,方程![]() 有且只有一个实数根,且
有且只有一个实数根,且![]() ,函数
,函数![]() 的图象与函数
的图象与函数![]() 的图象有三个不同的交点,则
的图象有三个不同的交点,则![]() 的取值范围为______________.
的取值范围为______________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱ABCD﹣A1B1C1D1中,底面ABCD为菱形,∠ABC=60°,AA1![]() AB,M,N分别为AB,AA1的中点.
AB,M,N分别为AB,AA1的中点.
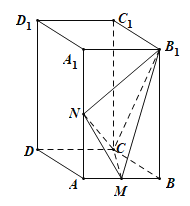
(1)求证:平面B1NC⊥平面CMN;
(2)若AB=2,求点N到平面B1MC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() -2为自然对数的底数,
-2为自然对数的底数,![]() ).
).
(1)若曲线![]() 在点
在点![]() 处的切线与曲线
处的切线与曲线![]() 至多有一个公共点时,求
至多有一个公共点时,求![]() 的取值范围;
的取值范围;
(2)当![]() 时,若函数
时,若函数![]() 有两个零点,求
有两个零点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com