
【题目】已知函数![]() .
.
(Ⅰ)求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)求![]() 的单调区间;
的单调区间;
(Ⅲ)若对于任意![]() ,都有
,都有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ) ![]() ;(Ⅱ)单调递增区间是
;(Ⅱ)单调递增区间是![]() ;
; ![]() 的单调递减区间是
的单调递减区间是![]() ;(Ⅲ)答案见解析.
;(Ⅲ)答案见解析.
【解析】试题分析:(Ⅰ)由f(1)=0,f′(1)=1;从而写出切线方程即可;
(Ⅱ)根据导数,求出导数等于0的根,分析导数函数值在根的左右的正负变化即可得出![]() 的单调区间;
的单调区间;
(Ⅲ)当![]() 时,“
时,“![]() ”等价于“
”等价于“![]() ”.令
”.令![]() ,
, ![]() ,求导研究单调性求出
,求导研究单调性求出![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,即可求出实数
,即可求出实数![]() 的取值范围.
的取值范围.
试题解析:
(Ⅰ)因为函数![]() ,
,
所以![]() ,
,
![]() .
.
又因为![]() ,
,
所以曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .
.
(Ⅱ)函数![]() 定义域为
定义域为![]() ,
,
由(Ⅰ)可知, ![]() .
.
令![]() 解得
解得![]() .
.
![]() 与
与![]() 在区间
在区间![]() 上的情况如下:
上的情况如下:
x |
|
|
|
|
|
|
|
| ↘ | 极小值 | ↗ |
所以, ![]() 的单调递增区间是
的单调递增区间是![]() ;
;
![]() 的单调递减区间是
的单调递减区间是![]() .
.
(Ⅲ)当![]() 时,“
时,“![]() ”等价于“
”等价于“![]() ”.
”.
令![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
当![]() 时,
时, ![]() ,所以
,所以![]() 在区间
在区间![]() 单调递减.
单调递减.
当![]() 时,
时, ![]() ,所以
,所以![]() 在区间
在区间![]() 单调递增.
单调递增.
而![]() ,
, ![]()
所以![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() .
.
所以当![]() 时,对于任意
时,对于任意![]() ,都有
,都有![]() .
.


科目:高中数学 来源: 题型:
【题目】对函数f(x)=xsinx,现有下列命题:①函数f(x)是偶函数;②函数f(x)的最小正周期是2π;③点(π,0)是函数f(x)的图象的一个对称中心;④函数f(x)在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减.其中是真命题的是________.(写出所有真命题的序号)
上单调递减.其中是真命题的是________.(写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了迎接第二届国际互联网大会,组委会对报名参加服务的![]() 名志愿者进行互联网知识测试,从这
名志愿者进行互联网知识测试,从这![]() 名志愿者中采用随机抽样的方法抽取
名志愿者中采用随机抽样的方法抽取![]() 人,所得成绩如下:
人,所得成绩如下: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(1)作出抽取的![]() 人的测试成绩的茎叶图,以频率为概率,估计这
人的测试成绩的茎叶图,以频率为概率,估计这![]() 志愿者中成绩不低于
志愿者中成绩不低于![]() 分的人数;
分的人数;
(2)从抽取的成绩不低于![]() 分的志愿者中,随机选
分的志愿者中,随机选![]() 名参加某项活动,求选取的
名参加某项活动,求选取的![]() 人恰有一人成绩不低于
人恰有一人成绩不低于![]() 分的概率.
分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知线段AB的端点B的坐标为(3,0),端点A在圆![]() 上运动;
上运动;
(1)求线段AB中点M的轨迹方程;
(2)过点C(1,1)的直线m与M的轨迹交于G、H两点,当△GOH(O为坐标原点)的面积最大时,求直线m的方程并求出△GOH面积的最大值.
(3)若点C(1,1),且P在M轨迹上运动,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了让贫困地区的孩子们过一个温暖的冬天,某校阳光志愿者社团组织“这个冬天不再冷”冬衣募捐活动,共有50名志愿者参与.志愿者的工作内容有两项:①到各班做宣传,倡议同学们积极捐献冬衣;②整理、打包募捐上来的衣物.每位志愿者根据自身实际情况,只参与其中的某一项工作.相关统计数据如下表所示:

(1)如果用分层抽样的方法从参与两项工作的志愿者中抽取5人,再从这5人中选2人,那么“至少有1人是参与班级宣传的志愿者”的概率是多少?
(2)若参与班级宣传的志愿者中有12名男生,8名女生,从中选出2名志愿者,用![]() 表示所选志愿者中的女生人数,写出随机变量
表示所选志愿者中的女生人数,写出随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某图书公司有一款图书的历史收益率(收益率=利润÷每本收入)的频率分布直方图如图所示:
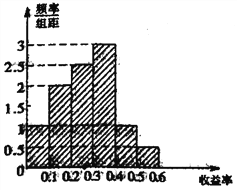
(1)试估计平均收益率;(用区间中点值代替每一组的数值)
(2)根据经验,若每本图书的收入在20元的基础上每增加![]() 元,对应的销量
元,对应的销量![]() (万份)与
(万份)与![]() (元)有较强线性相关关系,从历史销售记录中抽样得到如下5组
(元)有较强线性相关关系,从历史销售记录中抽样得到如下5组![]() 与
与![]() 的对应数据:
的对应数据:

据此计算出的回归方程为![]()
①求参数![]() 的估计值;
的估计值;
②若把回归方程![]() 当作
当作![]() 与
与![]() 的线性关系,
的线性关系, ![]() 取何值时,此产品获得最大收益,并求出该最大收益.
取何值时,此产品获得最大收益,并求出该最大收益.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥A-BCD中,AB=a,AC=AD=b,BC=CD=DB=c(a>0,b>0,c>0)该三棱锥的截面EFGH平行于AB、CD,分别交AD、AC、BC、BD于E、F、G、H.

(1)证明:AB⊥CD;
(2)求截面四边形EFGH面积的最大值,并说明面积取最大值时截面的位置.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com