
【题目】已知点![]() ,
,![]() 分别在
分别在![]() 轴,
轴,![]() 轴上运动,
轴上运动,![]() ,点
,点![]() 在线段
在线段![]() 上,且
上,且![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() ,若直线
,若直线![]() ,
,![]() 的斜率之和为2,直线
的斜率之和为2,直线![]() 是否恒过定点?若是,求出定点的坐标;若不是,请说明理由.
是否恒过定点?若是,求出定点的坐标;若不是,请说明理由.
【答案】(1)![]() (2)直线
(2)直线![]() 恒过定点
恒过定点![]()
【解析】
(1)设![]() ,由此得出
,由此得出![]() 两点的坐标,根据
两点的坐标,根据![]() 列方程,化简后求得
列方程,化简后求得![]() 点的轨迹方程.
点的轨迹方程.
(2)设![]() ,
,![]() ,当直线
,当直线![]() 斜率存在时,设直线
斜率存在时,设直线![]() 的方程为
的方程为![]() ,联立直线方程和轨迹
,联立直线方程和轨迹![]() 的方程,写出判别式和韦达定理,根据直线
的方程,写出判别式和韦达定理,根据直线![]() ,
,![]() 的斜率之和为2列方程,求得
的斜率之和为2列方程,求得![]() 的关系式,由此判断直线
的关系式,由此判断直线![]() 过点
过点![]() .当直线
.当直线![]() 斜率不存在时,同样利用直线
斜率不存在时,同样利用直线![]() ,
,![]() 的斜率之和为2列方程,由此求得直线
的斜率之和为2列方程,由此求得直线![]() 的方程,此时直线
的方程,此时直线![]() 也过点
也过点![]() ,由此判断出直线
,由此判断出直线![]() 恒过定点
恒过定点![]() .
.
(1)设![]() ,
,
因为点![]() 在线段
在线段![]() 上,且
上,且![]() ,所以
,所以![]() ,
,![]() ,
,
因为![]() ,所以
,所以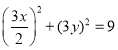 ,即
,即![]() ,
,
所以点![]() 的轨迹
的轨迹![]() 的方程为
的方程为![]() .
.
(2)设![]() ,
,![]() ,
,
当![]() 的斜率存在时,设
的斜率存在时,设![]() :
:![]() ,
,
由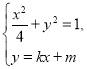 得
得![]() ,
,
所以![]() ,即
,即![]() ,
,
![]() ,
,![]() ,
,
因为直线![]() ,
,![]() 的斜率之和为2,所以
的斜率之和为2,所以![]() ,
,
所以![]() ,即
,即![]() ,所以
,所以![]() ,
,
当![]() 时,满足
时,满足![]() ,即
,即![]() ,符合题意,
,符合题意,
此时![]() :
:![]() 恒过定点
恒过定点![]() ,
,
当![]() 的斜率不存在时,
的斜率不存在时,![]() ,
,![]() ,
,
因为直线![]() ,
,![]() 的斜率之和为2,所以
的斜率之和为2,所以![]() ,
,
所以![]() ,此时
,此时![]() :
:![]() ,恒过定点
,恒过定点![]() ,
,
综上,直线![]() 恒过定点
恒过定点![]() .
.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:高中数学 来源: 题型:
【题目】如图,在三棱锥A﹣BCD中,点E在BD上,EA=EB=EC=ED,BD![]() CD,△ACD为正三角形,点M,N分别在AE,CD上运动(不含端点),且AM=CN,则当四面体C﹣EMN的体积取得最大值
CD,△ACD为正三角形,点M,N分别在AE,CD上运动(不含端点),且AM=CN,则当四面体C﹣EMN的体积取得最大值![]() 时,三棱锥A﹣BCD的外接球的表面积为_____.
时,三棱锥A﹣BCD的外接球的表面积为_____.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了更好地支持“中小型企业”的发展,某市决定对部分企业的税收进行适当的减免,某机构调查了当地的中小型企业年收入情况,并根据所得数据画出了样本的频率分布直方图,下面三个结论:
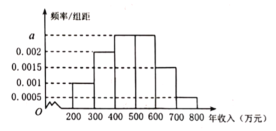
①样本数据落在区间![]() 的频率为0.45;
的频率为0.45;
②如果规定年收入在500万元以内的企业才能享受减免税政策,估计有55%的当地中小型企业能享受到减免税政策;
③样本的中位数为480万元.
其中正确结论的个数为( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在边长为2的等边![]() 中,
中,![]() 分别为边
分别为边![]() 的中点,将AED沿
的中点,将AED沿![]() 折起,使得
折起,使得![]() ,
, ![]() ,得到如图2的四棱锥A-BCDE,连结
,得到如图2的四棱锥A-BCDE,连结![]() ,且
,且![]() 与
与![]() 交于点
交于点![]() .
.
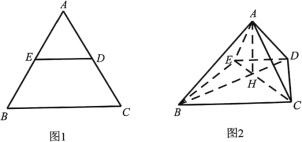
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列说法:①“![]() ”是“
”是“![]() ”的充分不必要条件;②命题“
”的充分不必要条件;②命题“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”;③小赵、小钱、小孙、小李到4个景点旅游,每人只去一个景点,设事件
”;③小赵、小钱、小孙、小李到4个景点旅游,每人只去一个景点,设事件![]() 为“4个人去的景点不相同”,事件
为“4个人去的景点不相同”,事件![]() 为“小赵独自去一个景点”,则
为“小赵独自去一个景点”,则![]() ;④设
;④设![]() ,其正态分布密度曲线如图所示,那么向正方形
,其正态分布密度曲线如图所示,那么向正方形![]() 中随机投掷10000个点,则落入阴影部分的点的个数的估计值是6587.(注:若
中随机投掷10000个点,则落入阴影部分的点的个数的估计值是6587.(注:若![]() ,则
,则![]() ,
,![]() )其中正确说法的个数为( )
)其中正确说法的个数为( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为椭圆
的焦点为椭圆![]() 的右焦点,C的准线与E交于P,Q两点,且
的右焦点,C的准线与E交于P,Q两点,且![]() .
.
(1)求E的方程;
(2)过E的左顶点A作直线l交E于另一点B,且BO(O为坐标原点)的延长线交E于点M,若直线AM的斜率为1,求l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex(x+1)2,令f1(x)=f'(x),fn+1(x)=fn'(x),若fn(x)=ex(anx2+bnx+cn),记数列{![]() }的前n项和为Sn,则下列选项中与S2019的值最接近的是( )
}的前n项和为Sn,则下列选项中与S2019的值最接近的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com