Question

【题目】如图，在四棱柱中，四边形ABCD为平行四边形，且点在底面上的投影H恰为CD的中点.

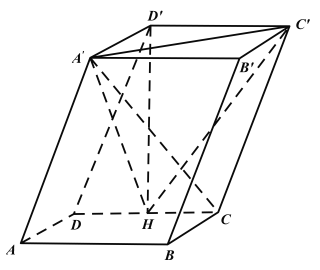
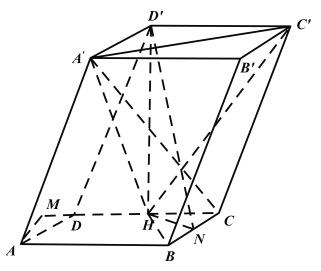
（1）棱BC上存在一点N，使得AD⊥平面，试确定点N的位置，说明理由；

（2）求三棱锥的体积.

Answer 1

【答案】（1）点N为棱BC的中点，理由见解析；（2）2.

【解析】

（1）点N为棱BC的中点，由题可得△HBC为等边三角形，所以NH⊥BC，又可证⊥BC，故可得BC⊥平面，又AD//BC，即证AD⊥平面；

（2）由题得到平面的距离即为A到平面的距离，过A作AM⊥CD于点M，证AM⊥平面，则，由条件代值计算即可.

（1）当点N为棱BC的中点时，符合题目要求，下面给出证明.

分别连结NH，，BH，

∵在底面上的投影H恰为CD的中点，∴⊥平面ABCD，

又BC平面ABCD，∴⊥BC，

在△HBC中，，故△HBC为等边三角形，

又点N为棱BC的中点，∴NH⊥BC，

又⊥BC，∩NH=H，，NH平面，

∴BC⊥平面，

又由平行四边形ABCD得AD//BC，

∴AD⊥平面，点N即为所求.

（2）∵平面//平面，

∴到面的距离即为A到平面的距离，

过A作AM⊥CD于点M，

又⊥平面ABCD，∴⊥AM，

又，∴AM⊥平面，

，，

又，

所以.