
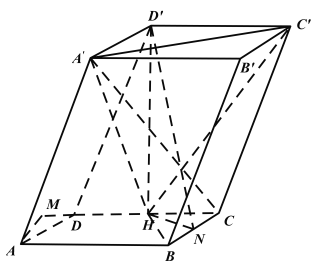
【题目】如图,在四棱柱![]() 中,四边形ABCD为平行四边形,
中,四边形ABCD为平行四边形,![]() 且点
且点![]() 在底面上的投影H恰为CD的中点.
在底面上的投影H恰为CD的中点.

(1)棱BC上存在一点N,使得AD⊥平面![]() ,试确定点N的位置,说明理由;
,试确定点N的位置,说明理由;
(2)求三棱锥![]() 的体积.
的体积.
【答案】(1)点N为棱BC的中点,理由见解析;(2)2.
【解析】
(1)点N为棱BC的中点,由题可得△HBC为等边三角形,所以NH⊥BC,又可证![]() ⊥BC,故可得BC⊥平面
⊥BC,故可得BC⊥平面![]() ,又AD//BC,即证AD⊥平面
,又AD//BC,即证AD⊥平面![]() ;
;
(2)由题得![]() 到平面
到平面![]() 的距离即为A到平面
的距离即为A到平面![]() 的距离,过A作AM⊥CD于点M,证AM⊥平面
的距离,过A作AM⊥CD于点M,证AM⊥平面![]() ,则
,则![]() ,由条件代值计算即可.
,由条件代值计算即可.
(1)当点N为棱BC的中点时,符合题目要求,下面给出证明.
分别连结NH,![]() ,BH,
,BH,
∵![]() 在底面上的投影H恰为CD的中点,∴
在底面上的投影H恰为CD的中点,∴![]() ⊥平面ABCD,
⊥平面ABCD,
又BC平面ABCD,∴![]() ⊥BC,
⊥BC,
在△HBC中,![]() ,故△HBC为等边三角形,
,故△HBC为等边三角形,
又点N为棱BC的中点,∴NH⊥BC,
又![]() ⊥BC,
⊥BC,![]() ∩NH=H,
∩NH=H,![]() ,NH平面
,NH平面![]() ,
,
∴BC⊥平面![]() ,
,
又由平行四边形ABCD得AD//BC,
∴AD⊥平面![]() ,点N即为所求.
,点N即为所求.
(2)∵平面![]() //平面
//平面![]() ,
,
∴![]() 到平面
到平面![]() 的距离即为A到平面
的距离即为A到平面![]() 的距离,
的距离,
过A作AM⊥CD于点M,
又![]() ⊥平面ABCD,∴
⊥平面ABCD,∴![]() ⊥AM,
⊥AM,
又![]() ,∴AM⊥平面
,∴AM⊥平面![]() ,
,
![]() ,
,![]() ,
,
又![]() ,
,
所以![]() .
.


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 为坐标原点,抛物线
为坐标原点,抛物线![]() 的焦点坐标为
的焦点坐标为![]() ,点
,点![]() ,
,![]() 在该抛物线上且位于
在该抛物线上且位于![]() 轴的两侧,
轴的两侧,![]() .
.
(Ⅰ)证明:直线![]() 过定点
过定点![]() ;
;
(Ⅱ)以![]() ,
,![]() 为切点作
为切点作![]() 的切线,设两切线的交点为
的切线,设两切线的交点为![]() ,点
,点![]() 为圆
为圆![]() 上任意一点,求
上任意一点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某“双一流A类”大学就业部从该校2018年已就业的大学本科毕业生中随机抽取了100人进行问卷调查,其中一项是他们的月薪收入情况,调查发现,他们的月薪收入在人民币1.65万元到2.35万元之间,根据统计数据分组,得到如下的频率分布直方图:

(1)为感谢同学们对这项调查工作的支持,该校利用分层抽样的方法从样本的前两组中抽出6人,各赠送一份礼品,并从这6人中再抽取2人,各赠送某款智能手机1部,求获赠智能手机的2人月薪都不低于1.75万元的概率;
(2)同一组数据用该区间的中点值作代表.
(i)求这100人月薪收入的样本平均数![]() 和样本方差
和样本方差![]() ;
;
(ii)该校在某地区就业的2018届本科毕业生共50人,决定于2019国庆长假期间举办一次同学联谊会,并收取一定的活动费用,有两种收费方案:
方案一:设![]() ,月薪落在区间
,月薪落在区间![]() 左侧的每人收取400元,月薪落在区间
左侧的每人收取400元,月薪落在区间![]() 内的每人收到600元,月薪落在区间
内的每人收到600元,月薪落在区间![]() 右侧的每人收取800元.
右侧的每人收取800元.
方案二:按每人一个月薪水的3%收取;用该校就业部统计的这100人月薪收入的样本频率进行估算,哪一种收费方案能收到更多的费用?
参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某玩具厂拟定生产两款新毛绒玩具样品,一款为毛绒小猪,另一款为毛绒小狗.由设计图知,生产这两款毛绒玩具均需相同材质的填充物、长毛绒、天鹅绒,且每个毛绒小猪需填充物![]() 、长毛绒
、长毛绒![]() 、天鹅绒
、天鹅绒![]() ,每个毛绒小狗需填充物
,每个毛绒小狗需填充物![]() 、长毛绒
、长毛绒![]() 、天鹅绒
、天鹅绒![]() .现有所需填充物
.现有所需填充物![]() 、长毛绒
、长毛绒![]() 、天鹅绒
、天鹅绒![]() ,若每个毛绒小猪与毛绒小狗的出厂价分别为64元、36元,则生这批毛绒玩具的最大销售额为_______元.
,若每个毛绒小猪与毛绒小狗的出厂价分别为64元、36元,则生这批毛绒玩具的最大销售额为_______元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱柱![]() 中,四边形ABCD为平行四边形,
中,四边形ABCD为平行四边形,![]() 且点
且点![]() 在底面上的投影H恰为CD的中点.
在底面上的投影H恰为CD的中点.
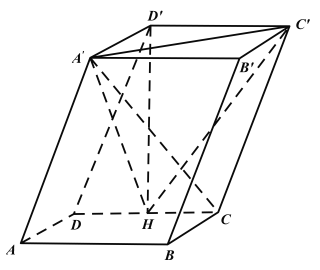
(1)棱BC上存在一点N,使得AD⊥平面![]() ,试确定点N的位置,说明理由;
,试确定点N的位置,说明理由;
(2)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年初,由于疫情影响,开学延迟,为了不影响学生的学习,国务院、省市区教育行政部门倡导各校开展“停学不停课、停学不停教”,某校语文学科安排学生学习内容包含老师推送文本资料学习和视频资料学习两类,且这两类学习互不影响已知其积分规则如下:每阅读一篇文本资料积1分,每日上限积5分;观看视频1个积2分,每日上限积6分.经过抽样统计发现,文本资料学习积分的概率分布表如表1所示,视频资料学习积分的概率分布表如表2所示.


(1)现随机抽取1人了解学习情况,求其每日学习积分不低于9分的概率;
(2)现随机抽取3人了解学习情况,设积分不低于9分的人数为ξ,求ξ的概率分布及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】海南盛产各种名贵树木,如紫檀、黄花梨等.在实际测量单根原木材体积时,可以检量木材的实际长度(检尺长)和小头直径(检尺径),再通过国家公布的原木材积表直接查询得到,原木材积表的部分数据如下所示:
检尺径 ( | 检尺长( | ||||
2.0 | 2.2 | 2.4 | 2.5 | 2.6 | |
材积( | |||||
8 | 0.0130 | 0.0150 | 0.0160 | 0.0170 | 0.0180 |
10 | 0.0190 | 0.0220 | 0.0240 | 0.0250 | 0.0260 |
12 | 0.0270 | 0.0300 | 0.0330 | 0.0350 | 0.0370 |
14 | 0.0360 | 0.0400 | 0.0450 | 0.0470 | 0.0490 |
16 | 0.0470 | 0.0520 | 0.0580 | 0.0600 | 0.0630 |
18 | 0.0590 | 0.0650 | 0.0720 | 0.0760 | 0.0790 |
20 | 0.0720 | 0.0800 | 0.0880 | 0.0920 | 0.0970 |
22 | 0.0860 | 0.0960 | 0.1060 | 0.1110 | 0.1160 |
24 | 0.1020 | 0.1140 | 0.1250 | 0.1310 | 0.1370 |
若小李购买了两根紫檀原木,一根检尺长为![]() ,检尺径为
,检尺径为![]() ,另一根检尺长为
,另一根检尺长为![]() ,检尺径为
,检尺径为![]() ,根据上表,可知两根原木的材积之和为______
,根据上表,可知两根原木的材积之和为______![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 的公差为
的公差为![]() ,前n项和为
,前n项和为![]() ,且满足____________.(从①
,且满足____________.(从①![]() );②
);②![]() 成等比数列;③
成等比数列;③![]() ,这三个条件中任选两个补充到题干中的横线位置,并根据你的选择解决问题)
,这三个条件中任选两个补充到题干中的横线位置,并根据你的选择解决问题)
(I)求![]() ;
;
(Ⅱ)若![]() ,求数列
,求数列![]() 的前n项和
的前n项和![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com