【题目】已知圆M的方程为x2+（y﹣2）2=1，直线l的方程为x﹣2y=0，点P在直线l上，过点P作圆M的切线PA，PB，切点为A，B．
（1）若点P的横坐标为1，求切线PA，PB的方程；
（2）若点P的纵坐标为a，且在圆M上存在点Q到点P的距离为1，求实数a的取值范围．
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目：高中数学 来源： 题型：
【题目】（1）双曲线
的离心率为_____________
（2）点P是椭圆
上一点，
分别是椭圆的左、右焦点，若
，则
的大小______ ．
（3）如果
是抛物线y2=4x上的点，它们的横坐标依次为
，F是抛物线的焦点，若
则
_______________．
（4）若x,y满足约束条件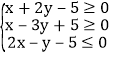
,则z=x2+y2的最大值为______________．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知数列{an}前n项和为Sn ， 满足Sn=2an﹣2n（n∈N*）．
（1）证明：{an+2}是等比数列，并求{an}的通项公式；
（2）数列{bn}满足bn=log2（an+2），Tn为数列{ 
}的前n项和，若Tn＜a对正整数a都成立，求a的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
的左、右顶点分别为A，B，直线l斜率大于0，且l经过椭圆的右焦点F，与椭圆交于两点P，Q，若△AFP，△BFQ的面积分别为S1，S2，若
，则直线l的斜率为_____．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设
，
是两条不同的直线， 
，
是两个不同的平面，则下列命题中正确的是
A. 若
，∥，∥, 则
B. 若，
，
，则
C. 若∥，
， 
，则
D. 若∥， ，
，则
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=ex（x2﹣a），a∈R．
（1）当a=1时，求曲线y=f（x）在点（0，f（0））处的切线方程；
（2）若函数f（x）在（﹣3，0）上单调递减，试求a的取值范围；
（3）若函数f（x）的最小值为﹣2e，试求a的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某化肥厂生产甲、乙两种混合肥料，需要A，B，C三种主要原料.生产1车皮甲种肥料和生产1车皮乙种肥料所需三种原料的吨数如下表所示：
现有A种原料200吨，B种原料360吨，C种原料300吨.在此基础上生产甲、乙两种肥料.已知生产1车皮甲种肥料，产生的利润为2万元；生产1车皮乙种肥料，产生的利润为3万元.分别用x，y表示计划生产甲、乙两种肥料的车皮数.
(1)用x，y列出满足生产条件的数学关系式，并画出相应的平面区域；
(2)问分别生产甲、乙两种肥料各多少车皮，能够产生最大的利润？并求出此最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
