练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在△ABC中，角A，B，C所对的边分别为a，b，c，已知．

    （1）求角B的大小；

    （2）若a+c=1，求b的取值范围．

    【答案】(1) ;(2) .

    【解析】试题分析; （1）已知等式利用正弦定理，整理后根据 不为0求出 的值，由 为三角形的内角，利用特殊角的三角函数值即可求出B的度数；
    （2）由余弦定理列出关系式，变形后将 及 的值代入表示出 ，根据的范围，利用二次函数的性质求出的范围，即可求出 的范围．

    试题解析：（1）由已知得： ， 由正弦定理，得 ，

    ∵sinA≠0，则 ， 即 ，又B∈（0，π），

    则B=.

    （2）∵a+c=1，即c=1﹣a，cosB=，∴由余弦定理得：b2=a2+c2﹣2accosB，即

    b2=a2+c2﹣ac=（a+c）2﹣3ac=1﹣3a（1﹣a）

    =3（a﹣）2+，由0＜a＜1，得≤b2＜1，∴≤b＜1．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】正项数列{an}前n项和为Sn ， 且 （n∈N+）
    （1）求数列{an}的通项公式；
    （2）若 ，数列{bn}的前n项和为Tn ， 证明：T2n﹣1＞1＞T2n（n∈N+）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，a、b、c分别为内角A、B、C的对边，且2asinA=（2b+c）sinB+（2c+b）sinC
    （1）求A的大小；
    （2）若sinB+sinC=1，试判断△ABC的形状．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】椭圆+=1的左、右焦点分别为F1，F2，一条直线经过点F1与椭圆交于A，B两点．

    （1）求△ABF2的周长；

    （2）若的倾斜角为，求弦长|AB|．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知关于x不等式x2﹣2mx+m+2<0（m∈R）的解集为M．

    （1）当M为空集时，求m的取值范围；

    （2）在（1）的条件下，求的最大值；

    （3）当M不为空集，且M [1，4]时，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数的定义域均为，且是奇函数，是偶函数，，其中为自然对数的底数.

    （1）求的解析式，并证明：当时，；

    （2）若关于的不等式在上恒成立，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量（吨）与相应的生产能耗（吨）标准煤的几组对照数据：

    （1）请画出上表数据的散点图；并指出是否线性相关；

    （2）请根据上表提供的数据，用最小二乘法求出关于的线性回归方程 ；

    （3）已知该厂技术改造前吨甲产品能耗为吨标准煤，试根据求出的线性回归方程，预测生产吨甲产品的生产能耗比技术改造前降低多少吨标准煤？

    （参考:用最小二乘法求线性回归方程系数公式 ，, .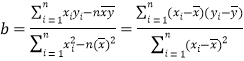

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知一个几何体的三视图如图所示.

    （1）求此几何体的表面积；

    （2）如果点在正视图中所示位置：为所在线段中点，为顶点，求在几何体表面上，从点到点的最短路径的长.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

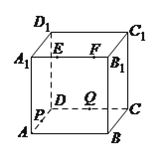
    【题目】如图，正方体的棱长为，动点、在棱上，动点，分别在棱，上，若，，，（，，大于零），则四面体的体积（ ）．

    A. 与，，都有关 B. 与有关，与，无关

    C. 与有关，与，无关 D. 与有关，与，无关

    查看答案和解析>>

    同步练习册答案