Question

【题目】如图所示（单位：cm），四边形ABCD是直角梯形，求图中阴影部分绕AB旋转一周所成几何体的表面积和体积．

Answer 1

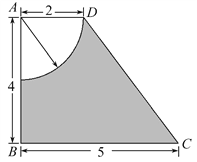
【答案】表面积为，体积为．

【解析】

试题分析：由题意知，所围成的几何体的表面积等于圆台的下底面积+圆台的侧面积+半球表面，该几何体的体积圆台的体积减去半个球的体积，由此可求出结果．

试题解析：由题意知，知所成几何体的表面积等于圆台下底面积＋圆台的侧面积＋半球面面积．

又S半球面＝×4π×22＝8π（cm2），

S圆台侧＝π（2＋5）＝35π（cm2），

S圆台下底＝π×52＝25π（cm2），

即该几何全的表面积为8π＋35π＋25π＝68π（cm2）．

又V圆台＝×（22＋2×5＋52）×4＝52π（cm3），V半球＝××23＝（cm3）．

所以该几何体的体积为V圆台－V半球＝52π－＝（cm3）．