
【题目】已知![]() 为公差不为零的等差数列,首项
为公差不为零的等差数列,首项![]() ,
, ![]() 的部分项
的部分项![]() 、
、![]() 、 、
、 、![]() 恰为等比数列,且
恰为等比数列,且![]() ,
,![]() ,
,![]() .
.
(1)求数列![]() 的通项公式
的通项公式![]() (用
(用![]() 表示);
表示);
(2)设数列![]() 的前
的前![]() 项和为
项和为![]() , 求证:
, 求证: ![]() (
(![]() 是正整数
是正整数
【答案】(1)![]() (2)见解析
(2)见解析
【解析】试题分析:
(1)由题得a1,a5,a17是成等比数列的,所以![]() ,则可以利用公差d和首项a来表示
,则可以利用公差d和首项a来表示![]() ,进而得到d的值,得到an的通项公式.
,进而得到d的值,得到an的通项公式.
(2)利用第一问可以求的等比数列![]() 、
、![]() 、 、
、 、![]() 中的前三项,得到该等比数列的通项公式,进而得到
中的前三项,得到该等比数列的通项公式,进而得到![]() 的通项公式,再利用分组求和法可得到Sn的表达式,可以发现
的通项公式,再利用分组求和法可得到Sn的表达式,可以发现![]() 为不可求和数列,所以需要把
为不可求和数列,所以需要把![]() 放缩成为可求和数列,考虑利用
放缩成为可求和数列,考虑利用![]() 的二项式定理放缩证明
的二项式定理放缩证明![]() ,即
,即![]() ,故求和即可证明原不等式.
,故求和即可证明原不等式.
试题解析:
(1)设数列![]() 的公差为
的公差为![]() ,
,
由已知得![]() ,
, ![]() ,
, ![]() 成等比数列,
成等比数列,
∴![]()
![]() ,且
,且![]() 2分
2分
得![]() 或
或![]()
∵ 已知![]() 为公差不为零
为公差不为零
∴![]() , 3分
, 3分
∴![]()
![]() . 4分
. 4分
(2)由(1)知![]() ∴
∴![]() 5分
5分
而等比数列![]() 的公比
的公比![]() .
.
∴![]() 6分
6分
因此![]()
![]() ,
,
∵![]()
∴![]() 7分
7分
∴![]()
![]()
![]() 9分
9分
∵当![]() 时,
时, ![]()
![]()
![]()
∴![]() (或用数学归纳法证明此不等式)
(或用数学归纳法证明此不等式)
∴![]()
![]() 11分
11分
∴当![]() 时,
时, ![]() ,不等式成立;
,不等式成立;
当![]() 时,
时, ![]()
![]()
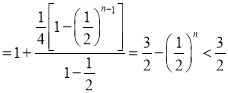
综上得不等式![]()
![]() 成立. 14分
成立. 14分
法二∵当![]() 时,
时, ![]()
![]()
![]()
∴![]() (或用数学归纳法证明此不等式)
(或用数学归纳法证明此不等式)
∴![]()
![]() 11分
11分
∴当![]() 时,
时, ![]() ,不等式成立;
,不等式成立;
当![]() 时,
时, ![]() ,不等式成立;
,不等式成立;
当![]() 时,
时, ![]()
![]()
![]()
综上得不等式![]()
![]() 成立. 14分
成立. 14分
(法三) 利用二项式定理或数学归纳法可得: ![]()
所以, ![]() 时,
时, ![]() ,
,
![]()
![]()
![]() 时,
时, ![]() 综上得不等式
综上得不等式![]()
![]() 成立.
成立.


科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() 为实数.
为实数.
(1)若关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() ,求实数
,求实数![]() 的值;
的值;
(2)设![]() ,当
,当![]() 时,求函数
时,求函数![]() 的最小值(用
的最小值(用![]() 表示);
表示);
(3)若关于![]() 不等式
不等式![]() 的解集中恰好有两个整数解,求
的解集中恰好有两个整数解,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】齐王与田忌赛马,田忌的上等马优于齐王的中等马,劣于齐王的上等马,田忌的中等马优于齐王的下等马,劣于齐王的中等马,田忌的下等马劣于齐王的下等马,现从双方的马匹中随机选一匹进行一场比赛,则田忌马获胜的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,以椭圆
,以椭圆![]() 的左顶点
的左顶点![]() 为圆心作圆
为圆心作圆![]() :
: ![]() ,设圆
,设圆![]() 与椭圆
与椭圆![]() 交于点
交于点![]() 与点
与点![]() .
.
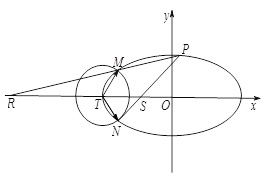
(1)求椭圆![]() 的方程;
的方程;
(2)求![]() 的最小值,并求此时圆
的最小值,并求此时圆![]() 的方程;
的方程;
(3)设点![]() 是椭圆
是椭圆![]() 上异于
上异于![]() ,
, ![]() 的任意一点,且直线
的任意一点,且直线![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,
, ![]() 为坐标原点,求证:
为坐标原点,求证: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)求证: ![]() .
.
(2)某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数:
sin213°+cos217°-sin13°cos17°;
sin215°+cos215°-sin15°cos15°;
sin218°+cos212°-sin18°cos12°;
sin2(-18°)+cos248°-sin(-18°)cos48°;
sin2(-25°)+cos255°-sin(-25°)cos55°.
①试从上述五个式子中选择一个,求出这个常数;
②根据①的计算结果,将该同学的发现推广为三角恒等式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某医药研究所开发了一种新药,如果成年人按规定的剂量服用,据监测,服药后每毫升血液中的含药量![]() (微克)与时间
(微克)与时间![]() (小时)之间的关系近似满足如图所示的曲线.
(小时)之间的关系近似满足如图所示的曲线.
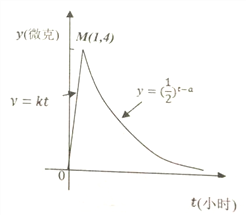
(1)写出服药后![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)据进一步测定:每毫升血液中含药量不少于0.25微克时,治疗疾病有效.求服药一次治疗疾病的有效时间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)是R上的偶函数,对x∈R都有f(x+4)=f(x)+f(2)成立.当x1,x2∈[0,2],且x1≠x2时,都有![]() <0,给出下列命题:
<0,给出下列命题:
①f(2)=0;
②直线x=-4是函数y=f(x)图象的一条对称轴;
③函数y=f(x)在[-4,4]上有四个零点;
④f(2 014)=0.
其中所有正确命题的序号为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com