
【题目】如图,已知四棱锥P-ABCD的底面是边长为1的正方形,且侧棱PC⊥底面ABCD,且PC=2,E是侧棱PC上的动点

(1)求四棱锥P-ABCD的体积;
(2)证明:BD⊥AE。
(3)求二面角P-BD-C的正切值。
【答案】(1)![]() (2)详见解析(3)
(2)详见解析(3)![]()
【解析】
试题分析:(1)四棱锥P-ABCD的体积V=![]() S正方形ABCDPC,由此能求出结果.(2)连结AC,由已知条件条件出BD⊥AC,BD⊥PC,从而得到BD⊥平面PAC,不论点E在何位置,都有AE平面PAC,由此能证明BD⊥AE.
S正方形ABCDPC,由此能求出结果.(2)连结AC,由已知条件条件出BD⊥AC,BD⊥PC,从而得到BD⊥平面PAC,不论点E在何位置,都有AE平面PAC,由此能证明BD⊥AE.
(3)以C为原点,CD为x轴,CB为y轴,CP为z轴,建立空间直角坐标系,利用向量法能求出二面角P-BD-C的正切值
试题解析:(1)该四棱锥P-ABCD的底面是边长为1的正方形,
侧棱PC⊥底面ABCD,且PC=2.
∴![]() …………4分
…………4分
(2)连结AC,∵ABCD是正方形
∴BD⊥AC ∵PC⊥底面ABCD 且![]() 平面
平面![]() ∴BD⊥PC …………6分
∴BD⊥PC …………6分
又∵![]() ∴BD⊥平面PAC
∴BD⊥平面PAC
∵不论点E在何位置,都有AE![]() 平面PAC
平面PAC
∴BD⊥AE …………8分
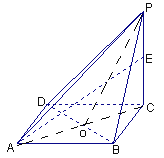
(3)设![]() 相交于
相交于![]() ,连
,连![]() ,由四棱锥P-ABCD的底面是边长为1的正方形,PC⊥底面ABCD知,
,由四棱锥P-ABCD的底面是边长为1的正方形,PC⊥底面ABCD知,![]() 是二面角P-BD-C的的一个平面角, …………10分
是二面角P-BD-C的的一个平面角, …………10分
![]() ,即二面角P-BD-C的正切值为
,即二面角P-BD-C的正切值为![]() .…………12分
.…………12分


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知方程![]() .
.
(1)求该方程表示一条直线的条件;
(2)当![]() 为何实数时,方程表示的直线斜率不存在?求出这时的直线方程;
为何实数时,方程表示的直线斜率不存在?求出这时的直线方程;
(3)已知方程表示的直线![]() 在
在![]() 轴上的截距为-3,求实数
轴上的截距为-3,求实数![]() 的值;
的值;
(4)若方程表示的直线![]() 的倾斜角是45°,求实数
的倾斜角是45°,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
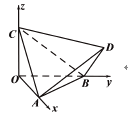
【题目】如图,正四面体![]() 的顶点
的顶点![]() 、
、![]() 、
、![]() 分别在两两垂直的三条射线
分别在两两垂直的三条射线![]() ,
, ![]() ,
, ![]() 上,则在下列命题中,错误的是( )
上,则在下列命题中,错误的是( )
A. ![]() 是正三棱锥
是正三棱锥
B. 直线![]() 与平面
与平面![]() 相交
相交
C. 直线![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]()
D. 异面直线![]() 和
和![]() 所成角是
所成角是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班一次数学考试成绩频率分布直方图如图所示,数据分组依次为![]() ,已知成绩大于等于
,已知成绩大于等于![]() 分的人数为
分的人数为![]() 人,现采用分层抽样的方式抽取一个容量为
人,现采用分层抽样的方式抽取一个容量为![]() 的样本.
的样本.
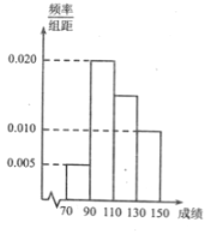
(1)求每个分组所抽取的学生人数;
(2)从数学成绩在![]() 的样本中任取
的样本中任取![]() 人,求恰有
人,求恰有![]() 人成绩在
人成绩在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合I={1,2,3,4,5},选择I的两个非空子集A和B,要使B中最小的数大于A中最大的数,则不同的选择方法共有
A.50种 B.49种 C.48种 D.47种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程,在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为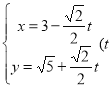 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系![]() 取相同的长度单位,且以原点
取相同的长度单位,且以原点![]() 为极轴,以
为极轴,以![]() 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆![]() 的方程为
的方程为![]() .
.
(1)求圆![]() 的圆心到直线
的圆心到直线![]() 的距离;
的距离;
(2)设圆![]() 与直线
与直线![]() 交于点
交于点![]() ,若点
,若点![]() 的坐标为
的坐标为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂有工人1000名,其中250名工人参加短期培训(称为![]() 类工人),另外750名工人参加过长期培训(称为
类工人),另外750名工人参加过长期培训(称为![]() 类工人).现用分层抽样方法(按
类工人).现用分层抽样方法(按![]() 类,
类,![]() 类分二层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(生产能力指一天加工的零件数).
类分二层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(生产能力指一天加工的零件数).
(1)![]() 类工人和
类工人和![]() 类工人中个抽查多少工人?
类工人中个抽查多少工人?
(2)从![]() 类工人中的抽查结果和从
类工人中的抽查结果和从![]() 类工人中的抽查结果分别如下表1和表2.
类工人中的抽查结果分别如下表1和表2.
表1:

表2:

① 先确定![]() ,
,![]() ,再完成下列频率分布直方图,就生产能力而言,
,再完成下列频率分布直方图,就生产能力而言,![]() 类工人中个体间的差异程度与
类工人中个体间的差异程度与![]() 类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)
类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)
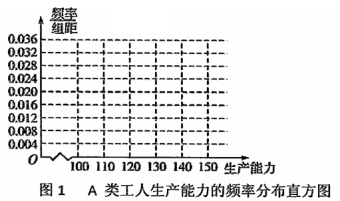
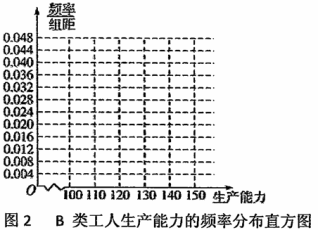
② 分别估计![]() 类工人和
类工人和![]() 类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数(同一组中
类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数(同一组中
的数据用该组区间的中点值作代表).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com