
����Ŀ��ij��ѧ���ڸ�һ��ѧ�ڿ�����Ӿѡ�Σ�Ϊ���˽��һѧ��ϲ����Ӿ�Ƿ����Ա��йأ���ѧУ��100����һ�����������ʾ����飬�õ�������������
ϲ����Ӿ | ��ϲ����Ӿ | �ϼ� | |
���� | 10 | ||
�� | 20 | ||
�ϼ� |
��֪����100���������ȡ1�˳鵽ϲ����Ӿ��ѧ���ĸ���Ϊ![]() ��
��
��1���뽫��������������������
��2�����ж��Ƿ���99.9%�İ�����Ϊϲ����Ӿ���Ա��йأ���˵��������ɣ�
��3����֪�ڱ������ѧ������5�����Լװ࣬����3��ϲ����Ӿ���ִ���5��ѧ���������ȡ2�ˣ���ǡ����1��ϲ����Ӿ�ĸ��ʣ�
������ٽ�ֵ�������ο���
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
���ο���ʽ�� ������
������![]() ��
��
���𰸡���1������������������2����![]() �İ�����Ϊϲ����Ӿ���Ա��йأ���3��
�İ�����Ϊϲ����Ӿ���Ա��йأ���3��![]() .
.
��������
�����������1�������������![]() ����������2�����ݸ����Ĺ�ʽ
����������2�����ݸ����Ĺ�ʽ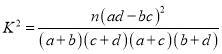 ������ϵ����ֵ���Ա��ٽ�ֵ������
������ϵ����ֵ���Ա��ٽ�ֵ������![]() ������
������![]() �İ�����Ϊϲ����Ӿ���Ա��йأ������أ���3��
�İ�����Ϊϲ����Ӿ���Ա��йأ������أ���3��![]() ��ѧ����ϲ����Ӿ��
��ѧ����ϲ����Ӿ��![]() ��ѧ����Ϊ
��ѧ����Ϊ![]() ������
������![]() ��ѧ����Ϊ
��ѧ����Ϊ![]() ����ȡ
����ȡ![]() ��ѧ�����г����п�������������ҳ�����
��ѧ�����г����п�������������ҳ�����![]() ��ѧ���������ȡ
��ѧ���������ȡ![]() �ˣ�ǡ����
�ˣ�ǡ����![]() ��ϲ����Ӿ����������ȼ�������ĸ���.
��ϲ����Ӿ����������ȼ�������ĸ���.
�����������1����Ϊ��100���������ȡ1�˳鵽ϲ����Ӿ��ѧ���ĸ���Ϊ![]() ��
��
����ϲ����Ӿ��ѧ������Ϊ![]() �ˣ�������������������������������������1��
�ˣ�������������������������������������1��
����Ů����20�ˣ���������40�ˣ��������������£�
ϲ����Ӿ | ��ϲ����Ӿ | �ϼ� | |
���� | 40 | 10 | 50 |
�� | 20 | 30 | 50 |
�ϼ� | 60 | 40 | 100 |
������������������������������������������������������������������������������������������������4��
��Ϊ![]() �������������������������������������� 7��
�������������������������������������� 7��
������99.9%�İ�����Ϊϲ����Ӿ���Ա��йأ�������������������������������������������8��
��2��5��ѧ����ϲ����Ӿ��3��ѧ����Ϊ![]() ������2��ѧ����Ϊ1��2����ȡ2��ѧ���������п������Ϊ
������2��ѧ����Ϊ1��2����ȡ2��ѧ���������п������Ϊ![]() ����10�֣�����������������10��
����10�֣�����������������10��
����ǡ��1��ϲ����Ӿ�Ŀ������Ϊ![]() ����6�֣��������������������� 11��
����6�֣��������������������� 11��
���ԣ�ǡ����1��ϲ����Ӿ�ĸ���Ϊ![]() ������������������������12��
������������������������12��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=x2+bx����b��0���ǡ�f��f��x��������Сֵ��f��x������Сֵ��ȡ��ģ� ��
A.��ֲ���Ҫ����
B.��Ҫ���������
C.��ֱ�Ҫ����
D.�Ȳ����Ҳ����Ҫ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�������غϵ�ֱ��![]() ���������غϵ�ƽ��
���������غϵ�ƽ��![]() ����
����![]() ���������ĸ����⣺����
���������ĸ����⣺����![]() ����
����![]() ������
������![]() ����
����![]() �� ����
�� ����![]() ����
����![]() ������
������![]() ����
����![]() ��������ȷ����ĸ����ǣ� ��
��������ȷ����ĸ����ǣ� ��
A. 0 B. 1 C. 2 D. 3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����![]() ����Բ
����Բ![]() ������
������![]() �Һ�ֱ��
�Һ�ֱ��![]() ���У��Ƕ�Բ��Բ��
���У��Ƕ�Բ��Բ��![]() �Ĺ켣Ϊ����
�Ĺ켣Ϊ����![]() .
.
��1��������![]() �ķ��̣�
�ķ��̣�
��2��������![]() ��һ��
��һ��![]() �ĺ�����Ϊ
�ĺ�����Ϊ![]() ����
����![]() ��ֱ�߽�
��ֱ�߽�![]() ��һ��
��һ��![]() ����
����![]() ���ڵ�
���ڵ�![]() ������
������![]() ��
��![]() �Ĵ��߽�
�Ĵ��߽�![]() ����һ��
����һ��![]() ����
����![]() ��
��![]() �����ߣ���
�����ߣ���![]() ����Сֵ.
����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ�����ȡ100��ѧ�����麮���ڼ�ѧ��ƽ��ÿ���ѧϰʱ�䣬�������ѧ��ÿ������ѧϰ��ʱ�����1Сʱ��11Сʱ֮�䣬��ѧ����ѧϰʱ��ֳ�5�飺��һ��![]() ���ڶ���
���ڶ���![]() ��������
��������![]() ��������
��������![]() ��������
��������![]() �����Ƴ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ��
�����Ƴ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ��
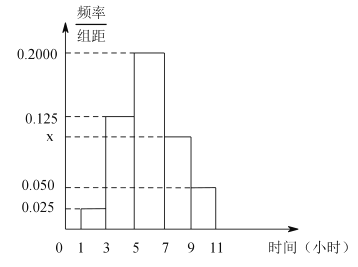
��1����ѧϰʱ����![]() ��ѧ��������
��ѧ��������
��2����Ҫ�ӵ����顢���������÷ֲ�����ķ�����ȡ6�ˣ�����6���������ȡ2�˽���ѧϰ�ĵã�����2����������1��ѧϰʱ���ڵ�����ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� ��֪����![]() ��aΪ������.
��a������.
����![]() ʱ������
ʱ������![]() �ĵ������䣻
�ĵ������䣻
����![]() ʱ������ʽ
ʱ������ʽ![]() ���������ʵ��
���������ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y=x2+��a+2��x��3��x��[a��b]��ͼ�����ֱ��x=1�Գƣ�
��1����a��b��ֵ�ͺ��������
��2��������f��x���Ķ�������[0��3]ʱ������f��x����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() �У�
�� ![]() ����
����![]() ������
������![]() ��ֱ�����Σ�
��ֱ�����Σ� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ����
����![]() ��
��![]() �ϣ���
�ϣ���![]() ��
��
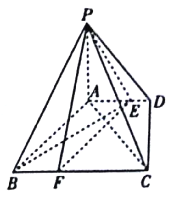
������֪��![]() ��
��![]() �ϣ���
�ϣ���![]() ����֤��ƽ��
����֤��ƽ��![]() ƽ��
ƽ��![]() ��
��
���������![]() ������ֵΪ����ʱ��ֱ��
������ֵΪ����ʱ��ֱ��![]() ��ƽ��
��ƽ��![]() ���ɵĽ�Ϊ
���ɵĽ�Ϊ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����ij�ֲ�Ʒ����̶��ɱ�Ϊ250��Ԫ��ÿ����![]() ǧ��������Ͷ��ɱ�Ϊ
ǧ��������Ͷ��ɱ�Ϊ![]() �������������80ǧ��ʱ��
�������������80ǧ��ʱ�� ![]() ����Ԫ��.���������С��80ǧ��ʱ��
����Ԫ��.���������С��80ǧ��ʱ�� ![]() ����Ԫ��.ÿ����Ʒ�ۼ�Ϊ0.05��Ԫ.ͨ���г��������ó���������Ʒ��ȫ������.
����Ԫ��.ÿ����Ʒ�ۼ�Ϊ0.05��Ԫ.ͨ���г��������ó���������Ʒ��ȫ������.
����д��������![]() ����Ԫ�����������
����Ԫ�����������![]() ��ǧ�����ĺ�������ʽ��
��ǧ�����ĺ�������ʽ��
���������Ϊ����ǧ��ʱ���ó�����һ��Ʒ�������������������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com