
【题目】已知椭圆方程是 ![]() =1,F1 , F2是它的左、右焦点,A,B为它的左、右顶点,l是椭圆的右准线,P是椭圆上一点,PA、PB分别交准线l于M,N两点.
=1,F1 , F2是它的左、右焦点,A,B为它的左、右顶点,l是椭圆的右准线,P是椭圆上一点,PA、PB分别交准线l于M,N两点.
(1)若P(0, ![]() ),求
),求 ![]() 的值;
的值;
(2)若P(x0 , y0)是椭圆上任意一点,求 ![]() 的值;
的值;
(3)能否将问题推广到一般情况,即给定椭圆方程是 ![]() =1(a>b>0),P(x0 , y0)是椭圆上任意一点,问
=1(a>b>0),P(x0 , y0)是椭圆上任意一点,问 ![]() 是否为定值?证明你的结论.
是否为定值?证明你的结论.
【答案】
(1)解:椭圆 ![]() =1的a=2,b=
=1的a=2,b= ![]() ,c=1,
,c=1,
可得A(﹣2,0),B(2,0),F1(﹣1,0),F2(1,0),右准线l:x=4,
由P(0, ![]() ),可得直线PA的方程为y=
),可得直线PA的方程为y= ![]() (x+2),令x=4,可得M(4,3
(x+2),令x=4,可得M(4,3 ![]() ),
),
同理可得N(4,﹣ ![]() ),
),
则 ![]() =(﹣1﹣4,﹣3
=(﹣1﹣4,﹣3 ![]() )(1﹣4,
)(1﹣4, ![]() )=﹣5×(﹣3)﹣3
)=﹣5×(﹣3)﹣3 ![]() ×
× ![]() =6
=6
(2)解:设P(x0,y0),则 ![]() +
+ ![]() =1,即y02=3(1﹣
=1,即y02=3(1﹣ ![]() ),
),
直线PA的方程为y= ![]() (x+2),(x0≠﹣2),
(x+2),(x0≠﹣2),
与x=4联立,可得M(4, ![]() ),同理可得N(4,
),同理可得N(4, ![]() ),
),
则 ![]() =(﹣5,﹣
=(﹣5,﹣ ![]() )(﹣3,﹣
)(﹣3,﹣ ![]() )=15+
)=15+ ![]()
=15+ 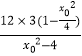 =15﹣9=6;
=15﹣9=6;
(3)解: ![]() 为定值2b2.
为定值2b2.
证明:由椭圆 ![]() =1,
=1,
可得A(﹣a,0),B(a,0),F1(﹣c,0),F2(c,0),右准线l:x= ![]() ,
,
设P(x0,y0),则 ![]() =1,即y02=b2(1﹣
=1,即y02=b2(1﹣ ![]() ),
),
直线PA的方程为y= ![]() (x+a),(x0≠﹣a),
(x+a),(x0≠﹣a),
与x= ![]() 联立,可得M(
联立,可得M( ![]() ,
, ![]() ),
),
同理可得N( ![]() ,
, ![]() ),
),
则 ![]() =(﹣c﹣
=(﹣c﹣ ![]() ,﹣
,﹣ ![]() )(c﹣
)(c﹣ ![]() ,﹣
,﹣ ![]() )
)
= ![]() ﹣c2+
﹣c2+ 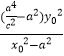 =
= ![]() +
+ ![]()
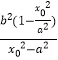
= ![]() ﹣
﹣ ![]() =
= ![]() =2b2
=2b2
【解析】(1)求得椭圆的a,b,c,可得顶点的坐标和焦点的坐标,求出直线PA的方程,求得M的坐标,同理可得N的坐标,运用向量的数量积的坐标表示,可得结论;(2)设P(x0 , y0),则 ![]() 1,即y02=3(1﹣
1,即y02=3(1﹣ ![]() ),求得直线PA的方程,可得M的坐标,以及N的坐标,运用向量的数量积的坐标表示,即可得到所求值6;(3)
),求得直线PA的方程,可得M的坐标,以及N的坐标,运用向量的数量积的坐标表示,即可得到所求值6;(3) ![]() 为定值2b2 . 设出椭圆的左右顶点和焦点,右准线方程,求得直线PA的方程,可得M的坐标和N的坐标,运用向量的数量积的坐标表示,化简整理,即可得到定值.
为定值2b2 . 设出椭圆的左右顶点和焦点,右准线方程,求得直线PA的方程,可得M的坐标和N的坐标,运用向量的数量积的坐标表示,化简整理,即可得到定值.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:高中数学 来源: 题型:
【题目】已知二次函数y=f(x)的图象过坐标原点,其导函数f′(x)=6x﹣2,数列{an}前n项和为Sn , 点(n,Sn)(n∈N*)均在y=f(x)的图象上.
(1)求数列{an}的通项公式;
(2)设 ![]() ,Tn是数列{bn}的前n项和,求当
,Tn是数列{bn}的前n项和,求当 ![]() 对所有n∈N*都成立m取值范围.
对所有n∈N*都成立m取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设事件A表示“关于x的一元二次方程x2+ax+b2=0有实根”,其中a,b为实常数. (Ⅰ)若a为区间[0,5]上的整数值随机数,b为区间[0,2]上的整数值随机数,求事件A发生的概率;
(Ⅱ)若a为区间[0,5]上的均匀随机数,b为区间[0,2]上的均匀随机数,求事件A发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的周长为l,面积为S,则△ABC的内切圆半径为r= ![]() .将此结论类比到空间,已知四面体ABCD的表面积为S,体积为V,则四面体ABCD的内切球的半径R= .
.将此结论类比到空间,已知四面体ABCD的表面积为S,体积为V,则四面体ABCD的内切球的半径R= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的函数f(x)满足f(x)+f(x+5)=16,当x∈(﹣1,4]时,f(x)=x2﹣2x , 则函数f(x)在区间[0,2016]上的零点个数是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,
中, ![]() :
: ![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系,已知曲线
轴正半轴为极轴建立极坐标系,已知曲线![]() .
.
(1)求![]() 的普通方程及
的普通方程及![]() 的直角坐标方程,并说明它们分别表示什么曲线;
的直角坐标方程,并说明它们分别表示什么曲线;
(2)若![]() 分别为
分别为![]() ,
, ![]() 上的动点,且
上的动点,且![]() 的最小值为2,求
的最小值为2,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com