练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】四棱锥中， ，且平面， ， ， 是棱的中点.

    （1）证明： 平面；

    （2）求二面角的余弦值.

    【答案】(1)证明见解析；(2) .

    【解析】试题分析：（1）取中点，连接、，四边形是平行四边形，通过证明面ACD,来证明平面。（2）取中点，过N点做BE的平行线为y轴，NB,NA分别为x,z轴建立空间直角坐标系，由空间向量求二面角的余弦值。

    试题解析：（1）取中点，连接、，

    ∵是中点，∴，且.

    又因为，∴.又∵，∴，∴四边形是平行四边形.∴，又，∴是等边三角形，∴，∵平面， ，∴平面，∴，∴平面，∴平面.

    （2）取中点，则， 平面，以为原点建立如图所示的直角坐标系.

    各点坐标为， ， ， ， ， .

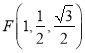    可得， ， ， ；

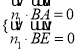    设平面的法向量，则得，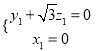

    取，

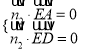    设平面的法向量，则得，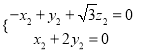

    取，

    于是 ，

    注意到二面角是钝角，因此，所求二面角的余弦值就是.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知抛物线的准线与轴交于点，过点作圆的两条切线，切点为，且.

    (1)求抛物线的方程；

    (2)若直线是过定点的一条直线，且与抛物线交于两点，过定点作的垂线与抛物线交于两点，求四边形面积的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在某中学举行的物理知识竞赛中，将三个年级参赛学生的成绩在进行整理后分成5组，绘制出如图所示的须率分布直方图，图中从左到右依次为第一、第二、第三、第四、第五小组.已知第三小组的频数是15.

    （1）求成绩在50-70分的频率是多少

    （2）求这三个年级参赛学生的总人数是多少：

    （3）求成绩在80-100分的学生人数是多少

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线的焦点为曲线的一个焦点， 为坐标原点，点为抛物线上任意一点，过点作轴的平行线交抛物线的准线于，直线交抛物线于点.

    （Ⅰ）求抛物线的方程；

    （Ⅱ）若、、三个点满足，求直线的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，

    （Ⅰ）当时，求函数的单调递减区间；

    （Ⅱ）若时，关于的不等式恒成立，求实数的取值范围；

    （Ⅲ）若数列满足， ，记的前项和为，求证： .

    【答案】（I）；（II）；（III）证明见解析.

    【解析】试题分析：（Ⅰ）求出，在定义域内，分别令求得的范围，可得函数增区间， 求得的范围，可得函数的减区间；（Ⅱ）当时，因为，所以显然不成立，先证明因此时， 在上恒成立，再证明当时不满足题意，从而可得结果；（III）先求出等差数列的前项和为，结合（II）可得，各式相加即可得结论.

    试题解析：（Ⅰ）由，得.所以

    令，解得或（舍去），所以函数的单调递减区间为 .

    （Ⅱ）由得，

    当时，因为，所以显然不成立，因此.

    令，则，令，得.

    当时， ， ，∴，所以，即有.

    因此时， 在上恒成立.

    ②当时， ， 在上为减函数，在上为增函数，

    ∴，不满足题意.

    综上，不等式在上恒成立时，实数的取值范围是.

    （III）证明：由知数列是的等差数列，所以

    所以

    由（Ⅱ）得， 在上恒成立.

    所以. 将以上各式左右两边分别相加，得

    .因为

    所以

    所以.

    【题型】解答题
    【/span>结束】
    22

    【题目】已知直线， (为参数， 为倾斜角).以坐标原点为极点， 轴的正半轴为极轴建立极坐标系，曲线的直角坐标方程为.

    （Ⅰ）将曲线的直角坐标方程化为极坐标方程；

    （Ⅱ）设点的直角坐标为，直线与曲线的交点为、，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】树立和践行“绿水青山就是金山银山，坚持人与自然和谐共生”的理念越来越深入人心，已形成了全民自觉参与，造福百姓的良性循环．据此，某网站退出了关于生态文明建设进展情况的调查，调查数据表明，环境治理和保护问题仍是百姓最为关心的热点，参与调查者中关注此问题的约占．现从参与关注生态文明建设的人群中随机选出200人，并将这200人按年龄分组：第1组，第2组，第3组，第4组，第5组，得到的频率分布直方图如图所示．

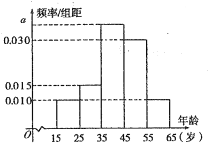
    （1）求出的值；

    （2）求这200人年龄的样本平均数（同一组数据用该区间的中点值作代表）和中位数（精确到小数点后一位）；

    （3）现在要从年龄较小的第1,2组中用分层抽样的方法抽取5人，再从这5人中随机抽取3人进行问卷调查，求这2组恰好抽到2人的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，平面平面， ， ， ， ， ．

    （Ⅰ）求证： ；

    （Ⅱ）求二面角的余弦值；

    （Ⅲ）若点在棱上，且平面，求线段的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)的导函数f '(x)的图象如图所示,f(-1)=f(2)=3,令g(x)=(x-1)f(x),则不等式g(x)≥3x-3的解集是( )

    A. [-1,1]∪[2,+∞)B. (-∞,-1]∪[1,2]

    C. (-∞,-1]∪[2,+∞)D. [-1,2]

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2020年寒假期间新冠肺炎肆虐，全国人民众志成城抗疫情.某市要求全体市民在家隔离，同时决定全市所有学校推迟开学.某区教育局为了让学生“停课不停学”，要求学校各科老师每天在网上授课辅导，每天共200分钟.教育局为了了解高三学生网上学习情况，上课几天后在全区高三学生中采取随机抽样的方法抽取了80名学生（其中男女生恰好各占一半）进行问卷调查，按男女生分为两组，再将每组学生在线学习时间（分钟）分为5组，，，，得到如图所示的频率分布直方图.全区高三学生有3000人（男女生人数大致相等），以频率估计概率回答下列问题：

    （1）估计全区高三学生中网上学习时间不超过40分钟的人数；

    （2）在调查的80名高三学生且学习时间不超过40分钟的学生中，男女生按分层抽样的方法抽取6人.若从这6人中随机抽取2人进行电话访谈，求至少抽到1名男生的概率.

    查看答案和解析>>

    同步练习册答案