
【题目】下列四个命题:①直线![]() 的斜率
的斜率![]() ,则直线
,则直线![]() 的倾斜角
的倾斜角![]() ;②直线
;②直线![]() :
:![]() 与以
与以![]() 、
、![]() 两点为端点的线段相交,则
两点为端点的线段相交,则![]() 或
或![]() ;③如果实数
;③如果实数![]() 满足方程
满足方程![]() ,那么
,那么![]() 的最大值为
的最大值为![]() ;④直线
;④直线![]() 与椭圆
与椭圆![]() 恒有公共点,则
恒有公共点,则![]() 的取值范围是
的取值范围是![]() .其中正确命题的序号是______
.其中正确命题的序号是______
【答案】②③
【解析】
由直线倾斜角的范围判断①错误;求出直线![]() 恒过的定点M,再求出MA和MB所在直线的斜率判断②正确;由
恒过的定点M,再求出MA和MB所在直线的斜率判断②正确;由![]() 的几何意义可知
的几何意义可知![]() 是连接圆上的动点和原点的连线的斜率,求出过原点的圆的切线的斜率判断③正确;由直线
是连接圆上的动点和原点的连线的斜率,求出过原点的圆的切线的斜率判断③正确;由直线![]() 恒过的定点在椭圆内部求解m的取值范围,结合圆的条件判断④错误.
恒过的定点在椭圆内部求解m的取值范围,结合圆的条件判断④错误.
对于①,由直线的倾斜角范围是![]() 知直线
知直线![]() 的斜率
的斜率![]() ,则直线
,则直线![]() 的倾斜角
的倾斜角![]() 错误;对于②,因为直线
错误;对于②,因为直线![]() 恒过点
恒过点![]() ,
,![]() ,所以
,所以![]() ,命题正确;对于③,方程
,命题正确;对于③,方程![]() 表示以
表示以![]() 为圆心,以
为圆心,以![]() 为半径的圆,
为半径的圆,![]() 的几何意义是连接圆上的动点和原点的连线的斜率,设过原点的圆的切线方程为
的几何意义是连接圆上的动点和原点的连线的斜率,设过原点的圆的切线方程为![]() ,由
,由![]() 得
得![]() ,所以
,所以![]() 的最大值为
的最大值为![]() ,命题正确;对于④,因为直线
,命题正确;对于④,因为直线![]() 恒过的定点
恒过的定点![]() ,所以要使直线与椭圆恒有公共点则需
,所以要使直线与椭圆恒有公共点则需![]() ,解得
,解得![]() ,但当
,但当![]() 时,方程
时,方程![]() 不是椭圆,所以命题错误.
不是椭圆,所以命题错误.
故答案为:②③


 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源: 题型:
【题目】学校艺术节对同一类的![]() ,
,![]() ,
,![]() ,
,![]() 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”;
作品获得一等奖”;
乙说:“![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“![]() ,
,![]() 两项作品未获得一等奖”;
两项作品未获得一等奖”;
丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
若这四位同学中只有两位说的话是对的,则获得一等奖的作品是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某地区2012年至2018年生活垃圾无害化处理量(单位:万吨)的折线图.
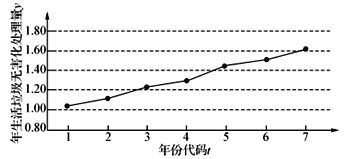
注:年份代码![]() 分别表示对应年份
分别表示对应年份![]() .
.
(1)由折线图看出,可用线性回归模型拟合![]() 与
与![]() 的关系,请用相关系数
的关系,请用相关系数![]() (
(![]() 线性相关较强)加以说明;
线性相关较强)加以说明;
(2)建立![]() 与
与![]() 的回归方程(系数精确到0.01),预测2019年该区生活垃圾无害化处理量.
的回归方程(系数精确到0.01),预测2019年该区生活垃圾无害化处理量.
(参考数据)![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(参考公式)相关系数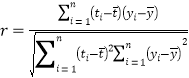 ,在回归方程
,在回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: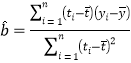 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
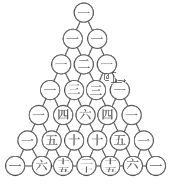
【题目】杨辉三角,又称帕斯卡三角,是二项式系数在三角形中的一种几何排列.在我国南宋数学家杨辉所著的《详解九章算法》(1261年)一书中用如图所示的三角形解释二项式乘方展开式的系数规律.现把杨辉三角中的数从上到下,从左到右依次排列,得数列:1,1,1,1,2,1,1,3,3,1,1,4,6,4,1…….记作数列![]() ,若数列
,若数列![]() 的前
的前![]() 项和为
项和为![]() ,则
,则![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一般来说,一个人脚掌越长,他的身高就越高,现对10名成年人的脚掌![]() 与身高
与身高![]() 进行测量,得到数据(单位:cm)作为样本如表所示:
进行测量,得到数据(单位:cm)作为样本如表所示:
脚掌长( | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 |
身高( | 141 | 146 | 154 | 160 | 169 | 176 | 181 | 188 | 197 | 203 |
(1)在上表数据中,以“脚掌长”为横坐标,“身高”为纵坐标,作出散点图后,发现散点在一条直线附近,试求“身高”与“脚掌长”之间的线性回归方程![]() ;
;
(2)若某人的脚掌长为26.5cm,试估计此人的身高;
(3)在样本中,从身高180cm以上的4人中随机抽取2人进行进一步的分析,求所抽取的2人中至少有1人身高在190cm以上的概率.
(参考数据: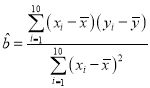 ,
, ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中已知A(4,O)、B(0,2)、C(-1,0)、D(0,-2),点E在线段AB(不含端点)上,点F在线段CD上,E、O、F三点共线.
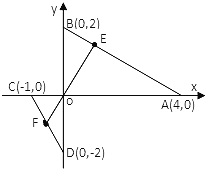
(1)若F为线段CD的中点,证明:![]() ;
;
(2)“若F为线段CD的中点,则![]() ”的逆命题是否成立?说明理由;
”的逆命题是否成立?说明理由;
(3)设![]() ,求
,求![]() 的值。
的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() ,
,![]() , O为DE的中点,
, O为DE的中点,![]() .F为
.F为![]() 的中点,平面
的中点,平面![]() 平面BCED.
平面BCED.
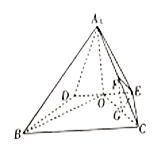
(1)求证:平面 ![]() 平面
平面![]() .
.
(2)线段OC上是否存在点G,使得![]() 平面EFG?说明理由。
平面EFG?说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司全年的纯利润为![]() 元,其中一部分作为奖金发给
元,其中一部分作为奖金发给![]() 位职工,奖金分配方案如下首先将职工工作业绩(工作业绩均不相同)从大到小,由1到
位职工,奖金分配方案如下首先将职工工作业绩(工作业绩均不相同)从大到小,由1到![]() 排序,第1位职工得奖金
排序,第1位职工得奖金![]() 元,然后再将余额除以
元,然后再将余额除以![]() 发给第2位职工,按此方法将奖金逐一发给每位职工,并将最后剩余部分作为公司发展基金.
发给第2位职工,按此方法将奖金逐一发给每位职工,并将最后剩余部分作为公司发展基金.
(1)设![]() 为第
为第![]() 位职工所得奖金额,试求
位职工所得奖金额,试求![]() 并用
并用![]() 和
和![]() 表示
表示![]() (不必证明);
(不必证明);
(2)证明![]() 并解释此不等式关于分配原则的实际意义;
并解释此不等式关于分配原则的实际意义;
(3)发展基金与![]() 和
和![]() 有关,记为
有关,记为![]() 对常数
对常数![]() ,当
,当![]() 变化时,求
变化时,求![]() .(可用公式
.(可用公式![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com