Question

【题目】在直角坐标系中已知A(4,O)、B(0,2)、C(-1,0)、D(0,-2),点E在线段AB(不含端点)上,点F在线段CD上,E、O、F三点共线.

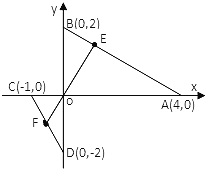
(1)若F为线段CD的中点,证明:；

(2)“若F为线段CD的中点,则”的逆命题是否成立?说明理由；

(3)设,求的值。

Answer 1

【答案】（1）见详解

（2）“若F为线段CD的中点,则”逆命题成立；

（3）

【解析】

（1）由条件求得，可得，再由可得；

（2）小题（1）的逆命题成立，设由得再得，由共线可得，解方程组，求得的坐标，可得F为线段CD的中点.

（3）设，由定比分点坐标公式可得，设，由定比分点坐标公式可得，再根据三点共线，可得， ，化简可得的值.

（1）

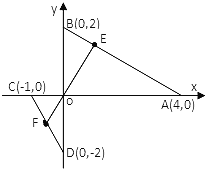
若F为线段CD的中点，则，

，

又

.

故

（2）小题（1）的逆命题成立，设，由，三点共线，可得，所以，

，

由共线，，，

所以，即

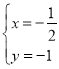解方程组 ，求得 ，可得

故F为线段CD的中点

（3） ，设，由定比分点坐标公式可得

，

设，由定比分点坐标公式可得

，

三点共线，可得，

即

，化简可得