
【题目】在如图所示的几何体中,四边形ABCD为正方形,△ABE为等腰直角三角形,∠BAE=90°,且AD⊥AE. 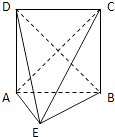
(1)证明:平面AEC⊥平面BED.
(2)求直线EC与平面BED所成角的正弦值.
【答案】
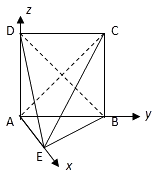
(1)证明:以A为原点,AE、AB、AD分别为x,y,z轴建立空间直角坐标系
设正方形边长为2,则E(2,0,0),B(0,2,0),C(0,2,2),D(0,0,2)
![]() =(0,2,2),
=(0,2,2), ![]() =(0,﹣2,2),
=(0,﹣2,2), ![]() =(2,0,0),
=(2,0,0), ![]() =(﹣2,0,2),
=(﹣2,0,2),
从而有 ![]() =0,
=0, ![]() =0,
=0,
即BD⊥AC,BD⊥AE,
因为AC∩AE=A,
所以BD⊥平面AEC,
因为BD平面BED,
所以平面BED⊥平面AEC
(2)解:设平面BED的法向量为 ![]() =(x,y,z),
=(x,y,z),
则 ![]() ,故取
,故取 ![]() =(1,1,1)
=(1,1,1)
而 ![]() =(﹣2,2,2),设直线EC与平面BED所成的角为θ,
=(﹣2,2,2),设直线EC与平面BED所成的角为θ,
则有sinθ=|cos< ![]() ,
, ![]() >|=
>|= 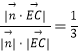
【解析】(1)以A为原点,AE、AB、AD分别为x,y,z轴建立空间直角坐标系,证明 ![]() =0,
=0, ![]() =0,可得BD⊥AC,BD⊥AE,即可证明BD⊥平面AEC,从而平面AEC⊥平面BED.(2)求出平面BED的法向量,利用向量的夹角公式,即可求直线EC与平面BED所成角的正弦值.
=0,可得BD⊥AC,BD⊥AE,即可证明BD⊥平面AEC,从而平面AEC⊥平面BED.(2)求出平面BED的法向量,利用向量的夹角公式,即可求直线EC与平面BED所成角的正弦值.
【考点精析】解答此题的关键在于理解平面与平面垂直的判定的相关知识,掌握一个平面过另一个平面的垂线,则这两个平面垂直,以及对空间角的异面直线所成的角的理解,了解已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则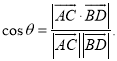 .
.


 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案科目:高中数学 来源: 题型:
【题目】某少数民族的刺绣有着悠久的历史,如图(1),(2),(3),(4)为最简单的四个图案,这些图案都是由小正方形构成,小正方形数越多刺绣越漂亮.现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形. 
(1)求出f(5)的值.
(2)利用合情推理的“归纳推理思想”,归纳出f(n+1)与f(n)之间的关系式,并根据你得到的关系式求出f(n)的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正三棱柱![]() 的各条棱长均相等,
的各条棱长均相等, ![]() 为
为![]() 的中点,
的中点, ![]() 分别是线段
分别是线段![]() 和线段
和线段![]() 上的动点(含端点),且满足
上的动点(含端点),且满足![]() .当
.当![]() 运动时,下列结论中不正确的是( )
运动时,下列结论中不正确的是( )
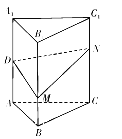
A. 平面![]() 平面
平面![]() B. 三棱锥
B. 三棱锥![]() 的体积为定值
的体积为定值
C. ![]() 可能为直角三角形 D. 平面
可能为直角三角形 D. 平面![]() 与平面
与平面![]() 所成的锐二面角范围为
所成的锐二面角范围为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,椭圆C: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,以原点为圆心,椭圆C的短半轴长为半径的圆与直线x﹣y+2=0相切.
,以原点为圆心,椭圆C的短半轴长为半径的圆与直线x﹣y+2=0相切. 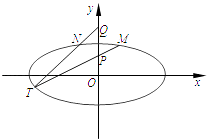
(1)求椭圆C的方程;
(2)已知点P(0,1),Q(0,2).设M,N是椭圆C上关于y轴对称的不同两点,直线PM与QN相交于点T,求证:点T在椭圆C上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某保险公司有一款保险产品的历史收益率(收益率=利润÷保费收入)的频率分布直方图如图所示:

(Ⅰ)试估计平均收益率;
(Ⅱ)根据经验,若每份保单的保费在20元的基础上每增加![]() 元,对应的销量
元,对应的销量![]() (万份)与
(万份)与![]() (元)有较强线性相关关系,从历史销售记录中抽样得到如下5组
(元)有较强线性相关关系,从历史销售记录中抽样得到如下5组![]() 与
与![]() 的对应数据:
的对应数据:

据此计算出的回归方程为![]() .
.
(i)求参数![]() 的估计值;
的估计值;
(ii)若把回归方程![]() 当作
当作![]() 与
与![]() 的线性关系,用(Ⅰ)中求出的平均收益率估计此产品的收益率,每份保单的保费定为多少元时此产品可获得最大收益,并求出该最大收益.
的线性关系,用(Ⅰ)中求出的平均收益率估计此产品的收益率,每份保单的保费定为多少元时此产品可获得最大收益,并求出该最大收益.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我市某矿山企业生产某产品的年固定成本为![]() 万元,每生产千件该产品需另投入
万元,每生产千件该产品需另投入![]() 万元,设该企业年内共生产此种产品
万元,设该企业年内共生产此种产品![]() 千件,并且全部销售完,每千件的销售收入为
千件,并且全部销售完,每千件的销售收入为![]() 万元,且
万元,且
(Ⅰ)写出年利润![]() (万元)关于产品年产量
(万元)关于产品年产量![]() (千件)的函数关系式;
(千件)的函数关系式;
(Ⅱ)问:年产量![]() 为多少千件时,该企业生产此产品所获年利润最大?
为多少千件时,该企业生产此产品所获年利润最大?
注:年利润=年销售收入-年总成本.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com