
分析 (Ⅰ)根据椭圆的简单几何性质,求出a、b的值即可;
(Ⅱ)当直线l的斜率存在时,求出直线RA、RB的斜率之和即可证明结论成立;
(Ⅲ)讨论直线l的斜率是否存在,利用弦长公式以及转化法、基本不等式等求出|AB|•|MN|的取值范围.
解答 解:(Ⅰ)因为椭圆C长轴长等于圆R:x2+(y-2)2=4的直径,
所以2a=4,a=2; …(1分)
由离心率为$\frac{\sqrt{2}}{2}$,得e2=$\frac{{c}^{2}}{{a}^{2}}$=$\frac{{a}^{2}{-b}^{2}}{{a}^{2}}$=$\frac{1}{2}$,
所以$\frac{{b}^{2}}{{a}^{2}}$=$\frac{{b}^{2}}{4}$=$\frac{1}{2}$,得b2=2;…(2分)
所以椭圆C的方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1;…(3分)
(Ⅱ)当直线l的斜率存在时,设l的方程为y=kx+1,与$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1联立,
消去y,得(1+2k2)x2+4kx-2=0;
设A(x1,y1),B(x2,y2),
则x1+x2=-$\frac{4k}{1+{2k}^{2}}$,x1x2=-$\frac{2}{1+{2k}^{2}}$,…(5分)
由R(0,2),得
kRA+kRB=$\frac{{y}_{1}-2}{{x}_{1}}$+$\frac{{y}_{2}-2}{{x}_{2}}$
=$\frac{{kx}_{1}-1}{{x}_{1}}$+$\frac{{kx}_{2}-1}{{x}_{2}}$
=2k-($\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$)
=2k-$\frac{{x}_{1}{+x}_{2}}{{{x}_{1}x}_{2}}$
=2k-$\frac{-\frac{4k}{1+{2k}^{2}}}{-\frac{2}{1+{2k}^{2}}}$=0.…(7分)
所以直线RA,RB的斜率之和等于零;…(8分)
(Ⅲ)当直线l的斜率不存在时,|AB|=2$\sqrt{2}$,|MN|=4,|AB|•|MN|=8$\sqrt{2}$;…(9分)
当直线l的斜率存在时,
|AB|=$\sqrt{{{(x}_{1}{-x}_{2})}^{2}{+{(y}_{1}{-y}_{2})}^{2}}$
=$\sqrt{1{+k}^{2}}$•|x1-x2|
=$\sqrt{1{+k}^{2}}$•$\sqrt{{{(x}_{1}{+x}_{2})}^{2}-{{4x}_{1}x}_{2}}$
=$\sqrt{1{+k}^{2}}$•$\sqrt{{(-\frac{4k}{1+{2k}^{2}})}^{2}+4×\frac{2}{1+{2k}^{2}}}$
=$\sqrt{1{+k}^{2}}$•$\frac{\sqrt{3{2k}^{2}+8}}{1+{2k}^{2}}$,
|MN|=2$\sqrt{4{-(\frac{1}{\sqrt{1{+k}^{2}}})}^{2}}$=2$\sqrt{\frac{{4k}^{2}+3}{1{+k}^{2}}}$,…(11分)
所以|AB|•|MN|=$\sqrt{1{+k}^{2}}$•$\frac{\sqrt{3{2k}^{2}+8}}{1+{2k}^{2}}$×2$\sqrt{\frac{{4k}^{2}+3}{1{+k}^{2}}}$
=4$\sqrt{2}$•$\frac{\sqrt{{4k}^{2}+1}\sqrt{{4k}^{2}+3}}{1+{2k}^{2}}$;
因为直线l过点P(0,1),所以直线l与椭圆C和圆R均交于两点,
令1+2k2=t,则t≥1,
所以|AB|•|MN|=4$\sqrt{2}$•$\sqrt{\frac{(2t-1)(2t+1)}{{t}^{2}}}$=4$\sqrt{2}$•$\sqrt{4-\frac{1}{{t}^{2}}}$<8$\sqrt{2}$,
又y=4$\sqrt{2}$•$\sqrt{4-\frac{1}{{t}^{2}}}$在t≥1时单调递增,
所以|AB|•|MN|=4$\sqrt{2}$$\sqrt{4-\frac{1}{{t}^{2}}}$≥4$\sqrt{6}$,
当且仅当t=1,k=0等号成立;…(13分)
综上,|AB|•|MN|的取值范围是[4$\sqrt{6}$,8$\sqrt{2}$].…(14分)
点评 本题考查了圆锥曲线的综合应用问题,也考查了数形结合思想、方程思想的应用问题,考查了计算能力与分析问题、解决问题的能力,是综合性题目.


科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,点P在正方体ABCD-A1B1C1D1的表面上运动,且P到直线BC与直线C1D1的距离相等,如果将正方体在平面内展开,那么动点P的轨迹在展开图中的形状是( )
如图,点P在正方体ABCD-A1B1C1D1的表面上运动,且P到直线BC与直线C1D1的距离相等,如果将正方体在平面内展开,那么动点P的轨迹在展开图中的形状是( )| A. | 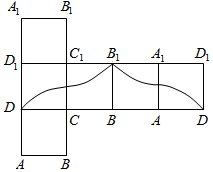 | B. |  | ||
| C. |  | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{1}{6}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{25}$ | B. | -$\frac{7}{25}$ | C. | -$\frac{24}{25}$ | D. | $\frac{24}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | π | D. | 2π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com