练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知菱形ABCD的边长为2，∠BAD=120°，点E、F分别在边BC、DC上， =λ ， =μ ，若 =1， =﹣ ，则λ+μ=（ ）
    A.
    B.
    C.
    D.

    【答案】C
    【解析】解：由题意可得若 =（ + ）（ + ）= + + +
    =2×2×cos120°+ +λ +λ μ =﹣2+4μ+4λ+λμ×2×2×cos120°
    =4λ+4μ﹣2λμ﹣2=1，
    ∴4λ+4μ﹣2λμ=3 ①．
    =﹣ （﹣ ）= =（1﹣λ） （1﹣μ） =（1﹣λ） （1﹣μ）
    =（1﹣λ）（1﹣μ）×2×2×cos120°=（1﹣λ﹣μ+λμ）（﹣2）=﹣ ，
    即﹣λ﹣μ+λμ=﹣ ②．
    由①②求得λ+μ= ，
    故答案为： ．

    利用两个向量的加减法的法则，以及其几何意义，两个向量的数量积的定义由 =1，求得4λ+4μ﹣2λμ=3 ①；再由 =﹣ ，求得﹣λ﹣μ+λμ=﹣ ②．结合①②求得λ+μ的值．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知是定义在上的奇函数，且，当a，，时，有成立．

    Ⅰ求在区间1上的最大值；

    Ⅱ若对任意的都有，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】禽流感一直在威胁我们的生活，某疾病控制中心为了研究禽流感病毒繁殖个数（个）随时间（天）变化的规律，收集数据如下：

    天数

    1

    2

    3

    4

    5

    6

    繁殖个数

    6

    12

    25

    49

    95

    190

    作出散点图可看出样本点分布在一条指数型函数的周围.

    保留小数点后两位数的参考数据：

    ，，，，，，，，其中

    （1）求出关于的回归方程（保留小数点后两位数字）；

    （2）已知，估算第四天的残差.

    参考公式：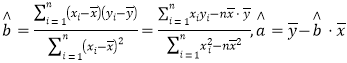

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】第一届“一带一路”国际合作高峰论坛于2017年5月14日至15日在北京举行，这是2017年我国重要的主场外交活动，对推动国际和地区合作具有重要意义．某高中政教处为了调查学生对“一带一路”的关注情况，在全校组织了“一带一路知多少”的知识问卷测试，并从中随机抽取了12份问卷，得到其测试成绩（百分制），如茎叶图所示．

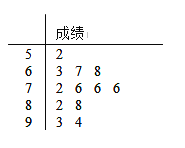
    （1）写出该样本的众数、中位数，若该校共有3000名学生，试估计该校测试成绩在70分以上的人数；

    （2）从所抽取的70分以上的学生中再随机选取4人．

    ①记表示选取4人的成绩的平均数，求；

    ②记表示测试成绩在80分以上的人数，求的分布和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

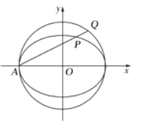
    【题目】如图，在平面直角坐标系中，已知椭圆 的离心率为，长轴长为4，过椭圆的左顶点作直线，分别交椭圆和圆于相异两点

    (1) 若直线的斜率为1，求的值:

    (2) 若，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列关于函数的判断正确的是（　　）

    ①的解集是；

    ②极小值，是极大值；

    ③没有最小值，也没有最大值．

    A. ①③ B. ①②③ C. ② D. ①②

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设椭圆 + =1（a＞b＞0）的左、右焦点分别为F1、F2 ， 右顶点为A，上顶点为B，已知|AB|= |F1F2|．
    （1）求椭圆的离心率；
    （2）设P为椭圆上异于其顶点的一点，以线段PB为直径的圆经过点F1 ， 经过原点O的直线l与该圆相切，求直线l的斜率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角梯形中， ， ， ， 分别为， 的中点，以为圆心， 为半径的圆交于，点在弧上运动（如图）.若，其中， ，则的取值范围是（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一个人有n把钥匙，其中只有一把可以打开房门，他随意的进行试开，若试开过的钥匙放在一边，试开次数X为随机变量，则P（X=k）=（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    同步练习册答案