
【题目】四川省双流中学是一所国家级示范高中,具有悠久的办学历史、丰富的办学经验.近年来,双中共为国内外高校输送合格新生20000余名,其中为清华、北大、复旦、人大等一流学府输送新生1800余名,上本科线人数年年超过千人,培养出省、市、县高考冠军17名,位居成都市同类学校前茅.该校高三某班有50名学生参加了今年成都市“一诊”考试,其中英语成绩服从正态分布![]() ,数学成绩的频率分布直方图如下:
,数学成绩的频率分布直方图如下:
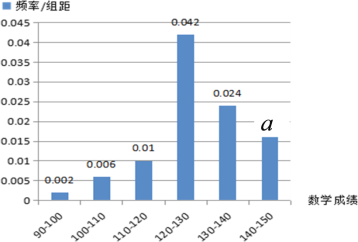
(1)如果成绩140分及以上为单科特优,则该班本次考试中英语、数学单科特优大约各多少人?
(2)试问该班本次考试中英语和数学平均成绩哪个较高,并说明理由;
(3)如果英语和数学两科都为单科特优共有5人,把(1)中的近似数作为真实值,从(1)中这些同学中随机抽取3人,设三人中英语和数学双科特优的有![]() 人,求
人,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考公式及数据:
![]() 则
则
![]()
![]()
![]()
【答案】(1)英语有![]() 人,数学有
人,数学有![]() 人;(2)数学,理由见解析;(3)分布列见解析,
人;(2)数学,理由见解析;(3)分布列见解析,![]()
【解析】
(1)由英语成绩服从正态分布![]() ,求出英语成绩为单科特优的概率为
,求出英语成绩为单科特优的概率为![]() ,由此能求出英语成绩为单科特优的同学的人数,由图形先求出
,由此能求出英语成绩为单科特优的同学的人数,由图形先求出![]() ,由此能求出数学成绩特优的同学的人数;
,由此能求出数学成绩特优的同学的人数;
(2)英语的平均价成绩为120人,数学的平均成绩为127分,从而数学的平均成绩更高;
(3)英语和数学双科特优的有5人,单科特优的有8人,得到![]() 的取值为
的取值为![]() ,分别求出相应的概率,由此求得随机变量
,分别求出相应的概率,由此求得随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
(1)由题意,英语成绩服从正态分布![]() ,
,
所以英语成绩为单科特优的概率为![]() ,
,
所以英语成绩为单科特优的同学约有![]() 人,
人,
因为![]() ,解得
,解得![]()
数学成绩特别优秀的同学约有![]() 人.
人.
(2)英语的平均成绩为120分,
数学的平均成绩为![]() 分,
分,
因为![]() ,所以数学的平均成绩更高.
,所以数学的平均成绩更高.
(3)英语和数学双科特优的有5人,单科特优的有8人,
从中抽取3人,随机变量![]() 可能取值有0,1,2,3,
可能取值有0,1,2,3,
![]() ;
;![]() ;
;
![]() ;
;![]()
故![]() 的分布列为:
的分布列为:
| 0 | 1 | 2 | 3 |
|
|
|
|
|
所以![]() 的数学期望为
的数学期望为![]() (人).
(人).


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】“二进制”来源于我国古代的《易经》,该书中有两类最基本的符号:“—”和“——”,其中“—”在二进制中记作“1”,“——”在二进制中记作“0”,例如二进制数![]() 化为十进制的计算如下:
化为十进制的计算如下:![]() .若从两类符号中任取2个符号进行排列,则得到的二进制数所对应的十进制数大于2的概率为( )
.若从两类符号中任取2个符号进行排列,则得到的二进制数所对应的十进制数大于2的概率为( )
A.0B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)求![]() 和
和![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 截直线
截直线![]() 所得线段的中点坐标为
所得线段的中点坐标为![]() ,求
,求![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新疆小南瓜以沙甜闻名全国,小田计划从新疆运输小南瓜去上海,随机从某瓜农的瓜地里挑选了100个,其质量分别在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:克)中,经统计得频率分布直方图如图所示,将频率视为概率.
(单位:克)中,经统计得频率分布直方图如图所示,将频率视为概率.
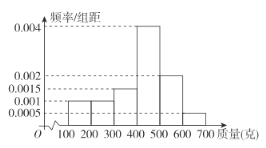
(1)请根据频率分布直方图估计该瓜农的小南瓜的平均质量;
(2)已知瓜地里还有2万个小南瓜已经成熟,可以采摘,小田想全部购买,可是瓜农要求超过400克的小南瓜以5元一个的价格出售,其他的以3元一个的价格出售.将频率视为概率,若新疆到上海往返的运费约2000元,请问这2万个小南瓜在上海以每斤(500克)多少元定价才能保证小田的利润不少于5000元?(结果保留一位小数)
(3)某天王阿姨在上海某超市的蔬菜柜台上看到小田从新疆采摘的新疆小南瓜,已知柜台上有若干个,若质量超过500克的小南瓜为“优质品”,王阿姨随机购买了20个小南瓜,求王阿姨购买的小南瓜中“优质品”个数的期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校![]() 名学生参加军事冬令营活动,活动期间各自扮演一名角色进行分组游戏,角色按级别从小到大共
名学生参加军事冬令营活动,活动期间各自扮演一名角色进行分组游戏,角色按级别从小到大共![]() 种,分别为士兵、排长、连长、营长、团长、旅长、师长、军长和司令.游戏分组有两种方式,可以
种,分别为士兵、排长、连长、营长、团长、旅长、师长、军长和司令.游戏分组有两种方式,可以![]() 人一组或者
人一组或者![]() 人一组.如果
人一组.如果![]() 人一组,则必须角色相同;如果
人一组,则必须角色相同;如果![]() 人一组,则
人一组,则![]() 人角色相同或者
人角色相同或者![]() 人为级别连续的
人为级别连续的![]() 个不同角色.已知这
个不同角色.已知这![]() 名学生扮演的角色有
名学生扮演的角色有![]() 名士兵和
名士兵和![]() 名司令,其余角色各
名司令,其余角色各![]() 人,现在新加入
人,现在新加入![]() 名学生,将这
名学生,将这![]() 名学生分成
名学生分成![]() 组进行游戏,则新加入的学生可以扮演的角色的种数为________.
组进行游戏,则新加入的学生可以扮演的角色的种数为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)解关于![]() 的不等式:
的不等式:![]() ;
;
(2)当![]() 时,过点
时,过点![]() 是否存在函数
是否存在函数![]() 图象的切线?若存在,有多少条?若不存在,说明理由;
图象的切线?若存在,有多少条?若不存在,说明理由;
(3)若![]() 是使
是使![]() 恒成立的最小值,试比较
恒成立的最小值,试比较![]() 与
与![]() 的大小(
的大小(![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,分别过椭圆![]() 左、右焦点
左、右焦点![]() 的动直线
的动直线![]() 相交于
相交于![]() 点,与椭圆
点,与椭圆![]() 分别交于
分别交于![]() 与
与![]() 不同四点,直线
不同四点,直线![]() 的斜率
的斜率![]() 满足
满足![]() .已知当
.已知当![]() 与
与![]() 轴重合时,
轴重合时,![]() ,
,![]() .
.
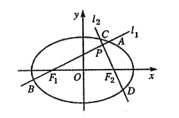
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)是否存在定点![]() ,使得
,使得![]() 为定值?若存在,求出
为定值?若存在,求出![]() 点坐标并求出此定值;若不存在,说明理由.
点坐标并求出此定值;若不存在,说明理由.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ,
,![]() 和
和![]() .
.
【解析】试题分析:(1)当![]() 与
与![]() 轴重合时,
轴重合时,![]() 垂直于
垂直于![]() 轴,得
轴,得![]() ,得
,得![]() ,
,![]() 从而得椭圆的方程;(2)由题目分析如果存两定点,则
从而得椭圆的方程;(2)由题目分析如果存两定点,则![]() 点的轨迹是椭圆或者双曲线 ,所以把
点的轨迹是椭圆或者双曲线 ,所以把![]() 坐标化,可得
坐标化,可得![]() 点的轨迹是椭圆,从而求得定点
点的轨迹是椭圆,从而求得定点![]() 和点
和点![]() .
.
试题解析:![]() 当
当![]() 与
与![]() 轴重合时,
轴重合时,![]() , 即
, 即![]() ,所以
,所以![]() 垂直于
垂直于![]() 轴,得
轴,得![]() ,
,![]() ,, 得
,, 得![]() ,
,![]() 椭圆
椭圆![]() 的方程为
的方程为![]() .
.
![]() 焦点
焦点![]() 坐标分别为
坐标分别为![]() , 当直线
, 当直线![]() 或
或![]() 斜率不存在时,
斜率不存在时,![]() 点坐标为
点坐标为![]() 或
或![]() ;
;
当直线![]()
![]() 斜率存在时,设斜率分别为
斜率存在时,设斜率分别为![]() , 设
, 设![]()
![]() 由
由 , 得:
, 得:
![]() , 所以:
, 所以:![]() ,
,![]() , 则:
, 则:
![]()
![]() . 同理:
. 同理:![]()
![]() , 因为
, 因为
![]() , 所以
, 所以![]()
![]() , 即
, 即![]() , 由题意知
, 由题意知![]() , 所以
, 所以
![]() , 设
, 设![]() ,则
,则![]() ,即
,即![]() ,由当直线
,由当直线![]() 或
或![]() 斜率不存在时,
斜率不存在时,![]() 点坐标为
点坐标为![]() 或
或![]() 也满足此方程,所以点
也满足此方程,所以点![]() 在椭圆
在椭圆![]() 上.存在点
上.存在点![]() 和点
和点![]() ,使得
,使得![]() 为定值,定值为
为定值,定值为![]() .
.
考点:圆锥曲线的定义,性质,方程.
【方法点晴】本题是对圆锥曲线的综合应用进行考查,第一问通过两个特殊位置,得到基本量![]() ,
,![]() ,得
,得![]() ,
,![]() ,从而得椭圆的方程,第二问由题目分析如果存两定点,则
,从而得椭圆的方程,第二问由题目分析如果存两定点,则![]() 点的轨迹是椭圆或者双曲线 ,本题的关键是从这个角度出发,把
点的轨迹是椭圆或者双曲线 ,本题的关键是从这个角度出发,把![]() 坐标化,求得
坐标化,求得![]() 点的轨迹方程是椭圆
点的轨迹方程是椭圆![]() ,从而求得存在两定点
,从而求得存在两定点![]() 和点
和点![]() .
.
【题型】解答题
【结束】
21
【题目】已知![]() ,
,![]() ,
,![]() .
.
(Ⅰ)若![]() ,求
,求![]() 的极值;
的极值;
(Ⅱ)若函数![]() 的两个零点为
的两个零点为![]() ,记
,记![]() ,证明:
,证明:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com