
【题目】已知函数![]() .
.
(1)解关于![]() 的不等式:
的不等式:![]() ;
;
(2)当![]() 时,过点
时,过点![]() 是否存在函数
是否存在函数![]() 图象的切线?若存在,有多少条?若不存在,说明理由;
图象的切线?若存在,有多少条?若不存在,说明理由;
(3)若![]() 是使
是使![]() 恒成立的最小值,试比较
恒成立的最小值,试比较![]() 与
与![]() 的大小(
的大小(![]() ).
).
【答案】(1)当![]() 时,
时,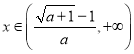 ;当
;当![]() 时,
时,![]() ;(2)不存在,理由见解析;(3)
;(2)不存在,理由见解析;(3)![]() .
.
【解析】
(1)当![]() 时,
时,![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() 时,
时,![]() ,解之即可;
,解之即可;
(2)由题意可得,切线斜率为![]() ,设
,设![]()
![]() ,求导可得
,求导可得![]() 在
在![]() 上递减,
上递减,![]() 上递增,故
上递增,故![]() ,所以方程无解,问题得解;
,所以方程无解,问题得解;
(3)由![]() 整理,得
整理,得![]() ,
,![]() 在
在![]() 上单调递增,最小值1,所以
上单调递增,最小值1,所以![]() ,即
,即![]() ,故
,故![]() ,
,![]() ,令
,令![]() ,可得
,可得![]() ,即可得出.
,即可得出.
(1)由已知![]() ,得
,得
当![]() 时,
时,![]() 的定义域为
的定义域为![]() ;当
;当![]() 时,
时,![]() 的定义域为
的定义域为![]()
①当![]() 时,
时,![]() ,原不等式等价于:
,原不等式等价于:
![]() ,
,
解得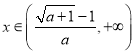 ;
;
②当![]() 时,
时,![]() ,原不等式等价于:
,原不等式等价于:
![]() ,
,
解得![]() .
.
(2)当![]() 时,
时,![]() ,
,
设![]() 上的切点坐标为
上的切点坐标为![]() ,显然
,显然![]() ,
,
求导,得![]() ,故切线斜率
,故切线斜率![]()
由题意,得![]() ,即
,即![]()
设![]() ,则
,则![]() ,
,
![]() 在
在![]() 上单调递减;在
上单调递减;在![]() 上单调递增,
上单调递增,
![]()
所以![]() 没有实根,故不存在切线.
没有实根,故不存在切线.
(3)由![]() 整理,得
整理,得![]()
由(2)可知,![]() 在
在![]() 上单调递增,
上单调递增,
所以当![]() 时
时![]() 取得最小值1,
取得最小值1,
由题意可得![]() ,即
,即![]() ,故
,故![]() ,
,
![]() .
.
令![]() ,则
,则![]() ,
,
而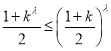 ,即
,即![]() ,
,
![]() ,
,
![]() .
.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:
【题目】已知项数为![]() 的数列
的数列![]() 满足如下条件:①
满足如下条件:①![]() ;②
;②![]() .若数列
.若数列![]() 满足
满足![]() ,其中
,其中![]() 则称
则称![]() 为
为![]() 的“心灵契合数列”.
的“心灵契合数列”.
(I)数列1,5,9,11,15是否存在“心灵契合数列”若存在,写出其心灵契合数列,若不存在请说明理由;
(II)若![]() 为
为![]() 的“心灵契合数列”,判断数列
的“心灵契合数列”,判断数列![]() 的单调性,并予以证明;
的单调性,并予以证明;
(Ⅲ)已知数列![]() 存在“心灵契合数列”
存在“心灵契合数列”![]() ,且
,且![]() ,
,![]() ,求m的最大值.
,求m的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|2x﹣a|+|x﹣a+1|.
(1)当a=4时,求解不等式f(x)≥8;
(2)已知关于x的不等式f(x)![]() 在R上恒成立,求参数a的取值范围.
在R上恒成立,求参数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四川省双流中学是一所国家级示范高中,具有悠久的办学历史、丰富的办学经验.近年来,双中共为国内外高校输送合格新生20000余名,其中为清华、北大、复旦、人大等一流学府输送新生1800余名,上本科线人数年年超过千人,培养出省、市、县高考冠军17名,位居成都市同类学校前茅.该校高三某班有50名学生参加了今年成都市“一诊”考试,其中英语成绩服从正态分布![]() ,数学成绩的频率分布直方图如下:
,数学成绩的频率分布直方图如下:
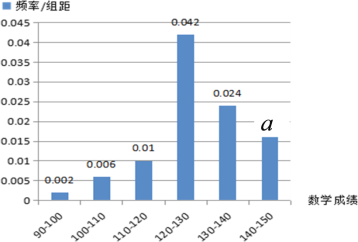
(1)如果成绩140分及以上为单科特优,则该班本次考试中英语、数学单科特优大约各多少人?
(2)试问该班本次考试中英语和数学平均成绩哪个较高,并说明理由;
(3)如果英语和数学两科都为单科特优共有5人,把(1)中的近似数作为真实值,从(1)中这些同学中随机抽取3人,设三人中英语和数学双科特优的有![]() 人,求
人,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考公式及数据:
![]() 则
则
![]()
![]()
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 与x轴负半轴交于
与x轴负半轴交于![]() ,离心率
,离心率![]() .
.
(1)求椭圆C的方程;
(2)设直线![]() 与椭圆C交于
与椭圆C交于![]() 两点,连接AM,AN并延长交直线x=4于
两点,连接AM,AN并延长交直线x=4于![]() 两点,若
两点,若![]() ,直线MN是否恒过定点,如果是,请求出定点坐标,如果不是,请说明理由.
,直线MN是否恒过定点,如果是,请求出定点坐标,如果不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
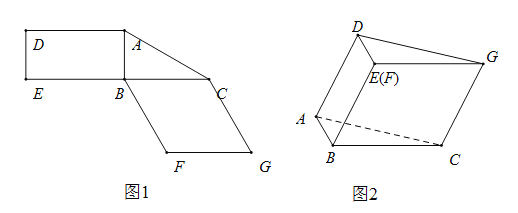
【题目】图1是由矩形ADEB,Rt△ABC和菱形BFGC组成的一个平面图形,其中AB=1,BE=BF=2,∠FBC=60°,将其沿AB,BC折起使得BE与BF重合,连结DG,如图2.
(1)证明:图2中的A,C,G,D四点共面,且平面ABC⊥平面BCGE;
(2)求图2中的二面角BCGA的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(某工厂生产零件A,工人甲生产一件零件A,是一等品、二等品、三等品的概率分别为![]() ,工人乙生产一件零件A,是一等品、二等品、三等品的概率分别为
,工人乙生产一件零件A,是一等品、二等品、三等品的概率分别为![]() .己知生产一件一等品、二等品、三等品零件A给工厂带来的效益分别为10元、5元、2元.
.己知生产一件一等品、二等品、三等品零件A给工厂带来的效益分别为10元、5元、2元.
(1)试根据生产一件零件A给工厂带来的效益的期望值判断甲乙技术的好坏;
(2)为鼓励工人提高技术,工厂进行技术大赛,最后甲乙两人进入了决赛.决赛规则是:每一轮比赛,甲乙各生产一件零件A,如果一方生产的零件A品级优干另一方生产的零件,则该方得分1分,另一方得分-1分,如果两人生产的零件A品级一样,则两方都不得分,当一方总分为4分时,比赛结束,该方获胜.Pi+4(i=![]() 4,
4,![]() 3,
3,![]() 2,…,4)表示甲总分为i时,最终甲获胜的概率.
2,…,4)表示甲总分为i时,最终甲获胜的概率.
①写出P0,P8的值;
②求决赛甲获胜的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
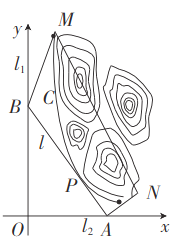
【题目】某贫困地区几个丘陵的外围有两条相互垂直的直线型公路![]() ,以及铁路线上的一条应开凿的直线穿山隧道
,以及铁路线上的一条应开凿的直线穿山隧道![]() ,为进一步改善山区的交通现状,计划修建一条连接两条公路
,为进一步改善山区的交通现状,计划修建一条连接两条公路![]() 和山区边界的直线型公路
和山区边界的直线型公路![]() , 以
, 以![]() 所在的直线分别为
所在的直线分别为![]() 轴,
轴,![]() 轴, 建立平面直角坐标系
轴, 建立平面直角坐标系![]() , 如图所示, 山区边界曲线为
, 如图所示, 山区边界曲线为![]() ,设公路
,设公路![]() 与曲线
与曲线![]() 相切于点
相切于点![]() ,
,![]() 的横坐标为
的横坐标为![]() .
.
(1)当![]() 为何值时,公路
为何值时,公路![]() 的长度最短?求出最短长度;
的长度最短?求出最短长度;
(2)当公路![]() 的长度最短时,设公路
的长度最短时,设公路![]() 交
交![]() 轴,
轴,![]() 轴分别为
轴分别为![]() ,
,![]() 两点,并测得四边形
两点,并测得四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 千米,
千米,![]() 千米,求应开凿的隧道
千米,求应开凿的隧道![]() 的长度.
的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com