
【题目】已知一动点![]() ,
, ![]() 到点
到点![]() 的距离减去它到
的距离减去它到![]() 轴距离的差都是
轴距离的差都是![]() .
.
(![]() )求动点
)求动点![]() 的轨迹方程.
的轨迹方程.
(![]() )设动点
)设动点![]() 的轨迹为
的轨迹为![]() ,已知定点
,已知定点![]() 、
、![]() ,直线
,直线![]() 、
、![]() 与轨迹
与轨迹![]() 的另一个交点分别为
的另一个交点分别为![]() 、
、![]() .
.
(i)点![]() 能否为线段
能否为线段![]() 的中点,若能,求出直线
的中点,若能,求出直线![]() 的方程,若不能,说明理由.
的方程,若不能,说明理由.
(ii)求证:直线![]() 过定点.
过定点.
【答案】(1) ![]() (2)①
(2)①![]() ②见解析
②见解析
【解析】试题分析:(1)由题意易得: ![]() ,坐标化易得动点
,坐标化易得动点![]() 的轨迹方程;(2)(i)设
的轨迹方程;(2)(i)设![]() ,
, ![]() ,
, ![]() ,假设
,假设![]() 能为
能为![]() 中点,则
中点,则![]() ,利用点在抛物线上可得
,利用点在抛物线上可得![]() ,
, ![]() 方程:
方程: ![]() ,∵
,∵![]() 与
与![]() 有两个交点,易得
有两个交点,易得![]() ,
, ![]() ,从而得到直线
,从而得到直线![]() 的方程;(ii)设
的方程;(ii)设![]() ,由
,由![]() :
:  得到
得到 ,同理可得:
,同理可得:  ,∴
,∴ ,从而得到直线
,从而得到直线![]() 过定点.
过定点.
试题解析:
(![]() )
)![]() ,
,  ,
,
 ,
, ![]() ,
,
∴![]() .
.
(![]() )
)
(i)设![]() ,
, ![]() ,
, ![]() ,
,
假设![]() 能为
能为![]() 中点,则
中点,则![]() ,
,
![]() ,
, ![]() 在轨迹方程上,则:
在轨迹方程上,则:
![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
,
![]() 方程:
方程: ![]() ,即
,即![]() ,
,
 ,
, ![]() 或
或![]() ,
,
∵![]() 与
与![]() 有两个交点,
有两个交点,
∴![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
,
∴![]() ,即
,即![]() ,
,
 ,
, ![]() ,
,
∴![]() 或
或![]() ,
,
∴![]() ,
, ![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() .
.
(ii)设![]() ,
,
∴![]() ,
,
![]() :
:  ,
,
![]() ,
,
![]() ,
,
![]() ,
,
∴![]() ,
,  ,
,
∴ ,
,
![]() :
:  ,
,
同理得: ![]() ,
,
![]() ,
,
∴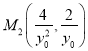 ,
,
 ,
,
整理可得: ![]() ,
,
∴![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
,
恒过![]() .
.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线的顶点是坐标原点![]() ,焦点
,焦点![]() 在
在![]() 轴的正半轴上,过焦点
轴的正半轴上,过焦点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与抛物线交于
与抛物线交于![]() 两点,且满足
两点,且满足![]() .
.
(1)求抛物线的方程;
(2)已知![]() 为抛物线上一点,若点
为抛物线上一点,若点![]() 位于
位于![]() 轴下方且
轴下方且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《城市规划管理意见》中提出“新建住宅原则上不再建设封闭住宅小区,已建成的住宅小区和单位大院逐步打开”,此消息在网上一石激起千层浪.各种说法不一而足,为了了解居民对“开放小区”认同与否,从[25,55]岁人群中随机抽取了n人进行问卷调查,得如下数据:
组数 | 分组 | 认同人数 | 认同人数占 |
第一组 | [25,30) | 120 | 0.6 |
第二组 | [30,35) | 195 | p |
第三组 | [35,40) | 100 | 0.5 |
第四组 | [40,45) | a | 0.4 |
第五组 | [45,50) | 30 | 0.3 |
第六组 | [50,55) | 15 | 0.3 |
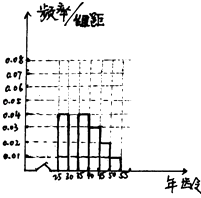
(1)完成所给频率分布直方图,并求n,a,p.
(2)若从[40,45),[45,50)两个年龄段中的“认同”人群中,按分层抽样的方法抽9人参与座谈会,然后从这9人中选2名作为组长,组长年龄在[40,45)内的人数记为ξ,求随机变量ξ的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两人同时生产内径为![]() 的一种零件,为了对两人的生产质量进行评比,从他们生产的零件中各抽出 5 件(单位:
的一种零件,为了对两人的生产质量进行评比,从他们生产的零件中各抽出 5 件(单位: ![]() ) ,
) ,
甲:25.44,25.43, 25.41,25.39,25.38
乙:25.41,25.42, 25.41,25.39,25.42.
从生产的零件内径的尺寸看、谁生产的零件质量较高.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了净化空气,某科研单位根据实验得出,在一定范围内,每喷洒1个单位的净化剂,空气中释放的浓度y(单位:毫克/立方米)随着时间x(单位:天)变化的函数关系式近似为y=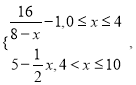 若多次喷洒,则某一时刻空气中的净化剂浓度为每次投放的净化剂在相应时刻所释放的浓度之和.由实验知,当空气中净化剂的浓度不低于4(毫克/立方米)时,它才能起到净化空气的作用.
若多次喷洒,则某一时刻空气中的净化剂浓度为每次投放的净化剂在相应时刻所释放的浓度之和.由实验知,当空气中净化剂的浓度不低于4(毫克/立方米)时,它才能起到净化空气的作用.
(1)若一次喷洒4个单位的净化剂,则净化时间可达几天?
(2)若第一次喷洒2个单位的净化剂,6天后再喷洒a(1≤a≤4)个单位的药剂,要使接下来的4天中能够持续有效净化,试求a的最小值(精确到0.1,参考数据: ![]() 取1.4).
取1.4).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设全集为R,集合A={x| ![]() ≥0},B={x|﹣2≤x<0},则(RA)∩B=( )
≥0},B={x|﹣2≤x<0},则(RA)∩B=( )
A.(﹣1,0)
B.[﹣1,0)
C.[﹣2,﹣1]
D.[﹣2,﹣1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=(x+1)lnx﹣a(x﹣1).
(1)若函数f(x)在x=e处的切线与y轴相交于点(0,2﹣e),求a的值;
(2)当1<x<2时,求证: ![]() >
> ![]() ﹣
﹣ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an},a1=1,且an﹣1﹣an﹣1an﹣an=0(n≥2,n∈N*),记bn=a2n﹣1a2n+1 , 数列{bn}的前n项和为Tn , 则满足不等式Tn< ![]() 成立的最大正整数n为 .
成立的最大正整数n为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com