
【题目】已知三棱锥![]() 的底面
的底面![]() 是等边三角形,点
是等边三角形,点![]() 在平面
在平面![]() 上的射影在
上的射影在![]() 内(不包括边界),
内(不包括边界),![]() .记
.记![]() ,
,![]() 与底面所成角为
与底面所成角为![]() ,
,![]() ;二面角
;二面角![]() ,
,![]() 的平面角为
的平面角为![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() 之间的大小关系等确定的是()
之间的大小关系等确定的是()
A. ![]() B.
B. ![]()
C. ![]() 是最小角,
是最小角,![]() 是最大角D. 只能确定
是最大角D. 只能确定![]() ,
,![]()
【答案】C
【解析】
过![]() 作PO⊥平面ABC,垂足为
作PO⊥平面ABC,垂足为![]() ,过
,过![]() 作OD⊥AB,交AB于D,过
作OD⊥AB,交AB于D,过![]() 作OE⊥BC,交BC于E,过
作OE⊥BC,交BC于E,过![]() 作OF⊥AC,交AC于F,推导出OA<OB<OC,AB=BC=AC,OD<OF<OE,且OE<OB,OF<OA,由此得到结论.
作OF⊥AC,交AC于F,推导出OA<OB<OC,AB=BC=AC,OD<OF<OE,且OE<OB,OF<OA,由此得到结论.
解:如图,过![]() 作PO⊥平面ABC,垂足为
作PO⊥平面ABC,垂足为![]() ,
,
过![]() 作OD⊥AB,交AB于D,
作OD⊥AB,交AB于D,
过![]() 作OE⊥BC,交BC于E,
作OE⊥BC,交BC于E,
过![]() 作OF⊥AC,交AC于F,
作OF⊥AC,交AC于F,
连结OA,OB,OC,PD,PE,PF,
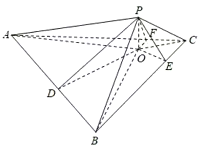
∵△ABC为正三角形,PA<PB<PC,
二面角PBCA,二面角PACB的大小分别为![]() ,
,![]() ,
,
PA,PB与底面所成角为![]() ,
,![]() ,
,
∴![]() =∠PAO,
=∠PAO,![]() =∠PBO,γ=∠PEO,
=∠PBO,γ=∠PEO,![]() =∠PFO,
=∠PFO,
OA<OB<OC,AB=BC=AC,
在直角三角形OAF中,![]() ,
,
在直角三角形OBE中,![]() ,
,
OA<OB,∠OAF<∠OBE,
则OF<OE,同理可得OD<OF,
∴OD<OF<OE,且OE<OB,OF<OA,
∴![]() <
<![]() ,
,![]() <
<![]() ,
,![]() >
>![]() ,
,![]() <
<![]() ,
,
可得![]() 是最小角,
是最小角,![]() 是最大角,
是最大角,
故选:C.


科目:高中数学 来源: 题型:
【题目】(本小题满分12分)已知椭圆![]() :
:![]() 的焦距为
的焦距为![]() ,离心率为
,离心率为![]() ,其右焦点为
,其右焦点为![]() ,过点
,过点![]() 作直线交椭圆于另一点
作直线交椭圆于另一点![]() .
.
(1)若![]() ,求
,求![]() 外接圆的方程;
外接圆的方程;
(2)若过点![]() 的直线与椭圆
的直线与椭圆![]()
![]() 相交于两点
相交于两点![]() 、
、![]() ,设
,设![]() 为
为![]() 上一点,且满足
上一点,且满足![]() (
(![]() 为坐标原点),当
为坐标原点),当![]() 时,求实数
时,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点F(1,0),O为坐标原点,A,B是抛物线C上异于 O的两点.
的焦点F(1,0),O为坐标原点,A,B是抛物线C上异于 O的两点.
(1)求抛物线C的方程;
(2)若直线AB过点(8,0),求证:直线OA,OB的斜率之积为定值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 经过点
经过点![]() ,且离心率为
,且离心率为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设![]() 是椭圆上的点,直线
是椭圆上的点,直线![]() 与
与![]() (
(![]() 为坐标原点)的斜率之积为
为坐标原点)的斜率之积为![]() .若动点
.若动点![]() 满足
满足![]() ,试探究是否存在两个定点
,试探究是否存在两个定点![]() ,使得
,使得![]() 为定值?若存在,求
为定值?若存在,求![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,PA垂直于以AB为直径的圆所在平面,C为圆上异于A,B的任意一点,![]() 垂足为E,点F是PB上一点,则下列判断中不正确的是( )﹒
垂足为E,点F是PB上一点,则下列判断中不正确的是( )﹒

A.![]() 平面PACB.
平面PACB.![]() C.
C.![]() D.平面
D.平面![]() 平面PBC
平面PBC
查看答案和解析>>
科目:高中数学 来源: 题型:
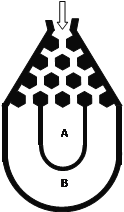
【题目】(本题满分12分)将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落.小球在下落过程中,将3次遇到黑色障碍物,最后落入![]() 袋或
袋或![]() 袋中.已知小球每次遇到黑色障碍物时向左、右两边下落的概率都是.
袋中.已知小球每次遇到黑色障碍物时向左、右两边下落的概率都是.
(Ⅰ)求小球落入![]() 袋中的概率
袋中的概率![]() ;
;
(Ⅱ)在容器入口处依次放入4个小球,记![]() 为落入
为落入![]() 袋中小球的个数,试求
袋中小球的个数,试求![]() 的概率和
的概率和![]() 的数学期望
的数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中华民族具有五千多年连绵不断的文明历史,创造了博大精深的中华文化,为人类文明进步作出了不可磨灭的贡献.为弘扬传统文化,某校组织了国学知识大赛,该校最终有四名选手![]() 、
、![]() 、
、![]() 、
、![]() 参加了总决赛,总决赛设置了一、二、三等奖各一个,无并列.比赛结束后,
参加了总决赛,总决赛设置了一、二、三等奖各一个,无并列.比赛结束后,![]() 对
对![]() 说:“你没有获得一等奖”,
说:“你没有获得一等奖”,![]() 对
对![]() 说:“你获得了二等奖”;
说:“你获得了二等奖”;![]() 对大家说:“我未获得三等奖”,
对大家说:“我未获得三等奖”,![]() 对
对![]() 、
、![]() 、
、![]() 说:“你妈三人中有一人未获奖”,四位选手中仅有一人撒谎,则选手获奖情形共计__________种.(用数字作答)
说:“你妈三人中有一人未获奖”,四位选手中仅有一人撒谎,则选手获奖情形共计__________种.(用数字作答)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com