
【题目】已知椭圆![]() 的左右顶点分别为A,B,离心率为
的左右顶点分别为A,B,离心率为![]() ,长轴长为4,动点S在C上位于x轴上方,直线
,长轴长为4,动点S在C上位于x轴上方,直线![]() 与直线
与直线![]() ,分别交于M,N两点.
,分别交于M,N两点.
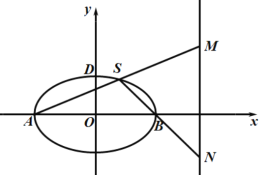
(1)求椭圆C的方程
(2)求|MN|的最小值
(3)当![]() 最小时,在椭圆C上是否存在这样的点T,使△TSB面积为
最小时,在椭圆C上是否存在这样的点T,使△TSB面积为![]() ?若存在,请确定点T的个数;若不存在,请说明理由
?若存在,请确定点T的个数;若不存在,请说明理由
【答案】(1)![]() ;(2)
;(2)![]() ;(3)4个点
;(3)4个点
【解析】
(1)根据离心率和长轴长可求得![]() ,即可求得椭圆的方程;
,即可求得椭圆的方程;
(2)用|![]() 表示MN|,再利用基本不等式求
表示MN|,再利用基本不等式求![]() 的最小值即可;
的最小值即可;
(3)求出![]() 的方程为
的方程为![]() ,与椭圆方程联立求得
,与椭圆方程联立求得![]() 的坐标,再设出与直线
的坐标,再设出与直线![]() 平行的直线方程,利用直线与椭圆相切时的三角形的面积与
平行的直线方程,利用直线与椭圆相切时的三角形的面积与![]() 进行比较,即可判断点
进行比较,即可判断点![]() 的个数.
的个数.
(1)![]()
![]() ,又
,又![]() ,
,
![]()
![]() ,
,![]() 椭圆的方程为
椭圆的方程为![]() .
.
(2)![]() ,
,![]()
又![]() ,
,
![]()
![]() ,
,![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,等号成立当且仅当
,等号成立当且仅当![]() .
.
(3)![]()
![]() ,
,![]()
![]() 的方程为
的方程为![]() ,与椭圆方程联立得:
,与椭圆方程联立得:
![]() ,
,![]()
![]() ,
,![]() ,
,
![]()
![]() ,
,
设与![]() 平行的直线为
平行的直线为![]() ,代入椭圆方程
,代入椭圆方程![]() ,
,
整理得:![]() ,
,
当直线与椭圆相切时,![]() ,
,
当![]() 时,点
时,点![]() 为切点,此时
为切点,此时![]() 的高为
的高为![]() ,
,
![]()
![]() 的面积为
的面积为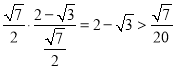 ,
,
![]() 在直线
在直线![]() 的上方存在两个点
的上方存在两个点![]() ,使得
,使得![]() 的面积为
的面积为![]() ,
,
当![]() 时,点
时,点![]() 为切点,此时
为切点,此时![]() 的高为
的高为![]() ,
,
![]()
![]() 的面积为
的面积为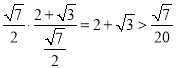 ,
,
![]() 在直线
在直线![]() 的下方存在两个点
的下方存在两个点![]() ,使得
,使得![]() 的面积为
的面积为![]() ,
,
![]() 椭圆C上存4个点T.
椭圆C上存4个点T.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案科目:高中数学 来源: 题型:
【题目】已知各项均为正数的两个数列![]() ,
,![]() 满足
满足![]() ,
,![]() .且
.且![]() .
.
(1)求证数列![]() 为等差数列;
为等差数列;
(2)求数列![]() 的通项公式;
的通项公式;
(3)设数列![]() ,
,![]() 的前n项和分别为
的前n项和分别为![]() ,
,![]() ,求使得等式
,求使得等式![]() 成立的有序数对
成立的有序数对![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知极点与直角坐标系的原点重合,极轴与![]() 轴的正半轴重合,曲线
轴的正半轴重合,曲线![]() 的极坐标方程是
的极坐标方程是![]() ,直线
,直线![]() 的参数方程是
的参数方程是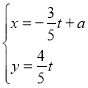 (
(![]() 为参数).
为参数).
(1)若![]() ,
,![]() 是圆
是圆![]() 上一动点,求点
上一动点,求点![]() 到直线
到直线![]() 的距离
的距离![]() 的最小值和最大值;
的最小值和最大值;
(2)直线![]() 与
与![]() 关于原点对称,且直线
关于原点对称,且直线![]() 截曲线
截曲线![]() 的弦长等于
的弦长等于![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x-1+![]() (a∈R,e为自然对数的底数).且曲线y=f(x)在点(1,f(1))处的切线平行于x轴.
(a∈R,e为自然对数的底数).且曲线y=f(x)在点(1,f(1))处的切线平行于x轴.
(1)求a的值;
(2)求函数f(x)的极值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市在开展创建“全国文明城市”活动中,工作有序扎实,成效显著,尤其是城市环境卫生大为改观,深得市民好评.“创文”过程中,某网站推出了关于环境治理和保护问题情况的问卷调查,现从参与问卷调查的人群中随机选出200人,并将这200人按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
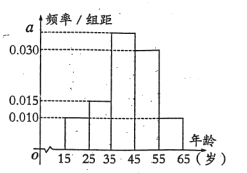
(1)求出a的值;
(2)若已从年龄较小的第1,2组中用分层抽样的方法抽取5人,现要再从这5人中随机抽取3人进行问卷调查,设第2组抽到![]() 人,求随机变量
人,求随机变量![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四面体A-BCD中,已知平面![]() 平面BCD,
平面BCD,![]() 为正三角形,
为正三角形,![]() 为等腰直角三角形,其中C为直角顶点,E,F分别为校AC,AD的中点.
为等腰直角三角形,其中C为直角顶点,E,F分别为校AC,AD的中点.
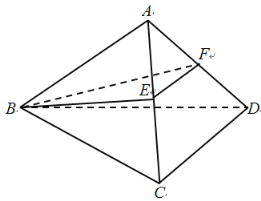
(1)求证:![]() 平面BEF;
平面BEF;
(2)求证:![]() 平面ACD.
平面ACD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() ,
,![]() ,平面
,平面![]() 平面PAD,E是
平面PAD,E是![]() 的中点,F是DC上一点,G是PC上一点,且
的中点,F是DC上一点,G是PC上一点,且![]() ,
,![]() .
.
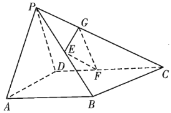
(1)求证:平面![]() 平面PAB;
平面PAB;
(2)若![]() ,
,![]() ,求直线PB与平面ABCD所成角的正弦值.
,求直线PB与平面ABCD所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com