
【题目】如图,已知多面体![]() 的底面
的底面![]() 是边长为2的菱形,
是边长为2的菱形, ![]() 底面
底面![]() ,
, ![]() ,且
,且![]() .
.
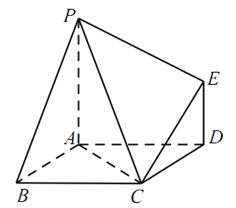
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)见解析(2) ![]()
【解析】试题分析: ![]() 连接
连接![]() ,交
,交![]() 于点
于点![]() ,设
,设![]() 中点为
中点为![]() ,连接
,连接![]() ,
, ![]() ,先证出
,先证出![]() ,再证出
,再证出![]() 平面
平面![]() ,,结合面面垂直的判定定理即可证平面
,,结合面面垂直的判定定理即可证平面![]() 平面
平面![]() ;
;
![]() 先证明
先证明![]() ,设
,设![]() 的中点为
的中点为![]() ,连接
,连接![]() ,所以点
,所以点![]() 到平面
到平面![]() 的距离与点
的距离与点![]() 到平面
到平面![]() 的距离相等,即
的距离相等,即![]() ,运用解三角形知识求其正弦值。
,运用解三角形知识求其正弦值。
解析:(1)证明:连接![]() ,交
,交![]() 于点
于点![]() ,设
,设![]() 中点为
中点为![]() ,连接
,连接![]() ,
, ![]() .
.
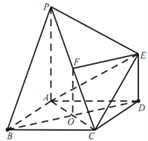
∵![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点,
的中点,
∴![]() ,且
,且![]() ,
,
∵![]() ,且
,且![]() ,
,
∴![]() ,且
,且![]() ,
,
∴四边形![]() 为平行四边形,∴
为平行四边形,∴![]() ,即
,即![]() ,
,
∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,∴
,∴![]() ,
,
∵![]() 是菱形,∴
是菱形,∴![]() .
.
∵![]() ,∴
,∴![]() 平面
平面![]() ,
,
∵![]() ,∴
,∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() .
.
(2)因为直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
所以![]() ,所以
,所以![]() ,
,
所以![]() ,故
,故![]() 为等边三角形,
为等边三角形,
设![]() 的中点为
的中点为![]() ,连接
,连接![]() ,则
,则![]()
![]() ,
,
设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,点
,点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
,
则由![]() ,得
,得![]() (*)
(*)
因为![]() 面
面![]() ,
, ![]() 面
面![]() ,所以
,所以![]() ,
,
又![]() ,
, ![]() ,∴
,∴![]() 面
面![]() ;
;
因为![]() ,
, ![]() 平面
平面![]() ,
, ![]() 面
面![]() ,所以
,所以![]() 面
面![]() ,
,
所以点![]() 到平面
到平面![]() 的距离与点
的距离与点![]() 到平面
到平面![]() 的距离相等,即
的距离相等,即![]() ,
,
因为![]() ,
, ![]() ,所以
,所以![]() ,
,
又![]() ,代入(*)得
,代入(*)得![]() ,所以
,所以![]() ,
,
设![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中数学 来源: 题型:
【题目】如图所示,在直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1,M,N分别是A1B,B1C1的中点.
(1)求证:MN⊥平面A1BC;
(2)求直线BC1和平面A1BC所成的角的大小.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)是定义在R上的偶函数,且满足f(x+2)=f(x).当x∈[0,1]时,f(x)=2x.若在区间[﹣2,3]上方程ax+2a﹣f(x)=0恰有四个不相等的实数根,则实数a的取值范围是( )
A.( ![]() ,
, ![]() )
)
B.( ![]() ,
, ![]() )
)
C.( ![]() ,2)
,2)
D.(1,2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电台在因特网上就观众对某一节目的喜爱程度进行调查,参加调查的总人数为12000人,其中持各种态度的人数如下表:
很喜爱 | 喜爱 | 一般 | 不喜爱 |
2435 | 4567 | 3926 | 1072 |
电视台为进一步了解观众的具体想法和意见,打算从中抽取60人进行更为详细的调查,应当怎样进行抽样?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 满足:
满足: ![]() ,且该函数的最小值为1.
,且该函数的最小值为1.
(1)求此二次函数![]() 的解析式;
的解析式;
(2)若函数![]() 的定义域为
的定义域为![]() (其中
(其中![]() ),问是否存在这样的两个实数
),问是否存在这样的两个实数![]() ,
, ![]() ,使得函数
,使得函数![]() 的值域也为
的值域也为![]() ?若存在,求出
?若存在,求出![]() ,
, ![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(3)若对于任意的![]() ,总存在
,总存在![]() 使得
使得![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px(p>0)的焦点为F,点M(x0 , 2 ![]() )(x0>
)(x0> ![]() )是抛物线C上一点,圆M与线段MF相交于点A,且被直线x=
)是抛物线C上一点,圆M与线段MF相交于点A,且被直线x= ![]() 截得的弦长为
截得的弦长为 ![]() |MA|,若
|MA|,若 ![]() =2,则|AF|等于( )
=2,则|AF|等于( )
A.![]()
B.1
C.2
D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com