
【题目】若数列![]() 、
、![]() 满足
满足![]() (
(![]() N*),则称
N*),则称![]() 为数列
为数列![]() 的“偏差数列”.
的“偏差数列”.
(1)若![]() 为常数列,且为
为常数列,且为![]() 的“偏差数列”,试判断
的“偏差数列”,试判断![]() 是否一定为等差数列,并说明理由;
是否一定为等差数列,并说明理由;
(2)若无穷数列![]() 是各项均为正整数的等比数列,且
是各项均为正整数的等比数列,且![]() ,
,![]() 为数列
为数列![]() 的“偏差数列”,求
的“偏差数列”,求![]() 的值;
的值;
(3)设![]() ,
,![]() 为数列
为数列![]() 的“偏差数列”,
的“偏差数列”,![]() ,
,![]() 且
且![]() ,若
,若![]() 对任意
对任意![]() 恒成立,求实数M的最小值.
恒成立,求实数M的最小值.
【答案】(1)见解析;(2)![]() 或
或![]() ;(3)
;(3)![]()
【解析】
(1){an}不一定为等差数列,如![]() ;
;
(2)设数列{an}的公比为q,解方程可得首项和公比,由等比数列的通项公式和求和公式,计算可得所求值;
(3)由累加法可得数列{an}的通项公式,讨论n为奇数或偶数,求得极限,由不等式恒成立思想可得M的最小值.
解:(1) 如![]() ,则
,则![]() 为常数列,但
为常数列,但![]() 不是等差数列,
不是等差数列,
(2) 设数列![]() 的公比为
的公比为![]() ,则由题意,
,则由题意,![]() 、
、![]() 均为正整数,
均为正整数,
因为![]() ,所以
,所以![]() ,
,
解得![]() 或
或![]() ,
,
故![]() 或
或![]() (
(![]() N*),
N*),
①当![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,
② 当![]() 时,
时,![]() ,
,![]() ,
,![]()
综上,![]() 的值为
的值为![]() 或
或![]() ;
;
(3) 由![]() ≤
≤![]() 且
且![]() ≤
≤![]() 得,
得,![]() =
=![]()
故有:![]() ,
,
![]() ,
,
![]() ,
,
累加得: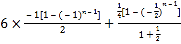
=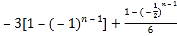
=![]() ,
,
又![]() ,所以
,所以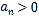
当n为奇数时,![]() 单调递增,
单调递增,![]() ,
,![]() ,
,
当n为偶数时,![]() 单调递减,
单调递减,![]() ,
,![]() ,
,
从而![]() ≤
≤![]() ,所以M≥
,所以M≥![]() ,即M的最小值为
,即M的最小值为![]() .
.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:高中数学 来源: 题型:
【题目】
在直角坐标系![]() 中,点P到两点
中,点P到两点![]() ,
,![]() 的距离之和等于4,设点P的轨迹为
的距离之和等于4,设点P的轨迹为![]() ,直线
,直线![]() 与C交于A,B两点.
与C交于A,B两点.
(Ⅰ)写出C的方程;
(Ⅱ)若![]()
![]()
![]() ,求k的值;
,求k的值;
(Ⅲ)若点A在第一象限,证明:当k>0时,恒有|![]() |>|
|>|![]() |.
|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用长为18 cm的钢条围成一个长方体形状的框架,要求长方体的长与宽之比为2:1,问该长方体的长、宽、高各为多少时,其体积最大?最大体积是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分12分)如图, ![]() 是圆
是圆![]() 的直径,点
的直径,点![]() 是圆
是圆![]() 上异于
上异于![]() 的点,
的点, ![]() 垂直于圆
垂直于圆![]() 所在的平面,且
所在的平面,且![]() .
.
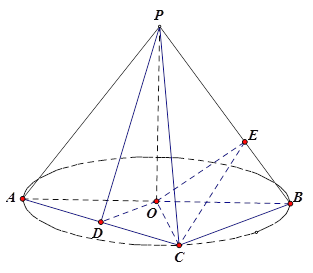
(Ⅰ)若![]() 为线段
为线段![]() 的中点,求证
的中点,求证![]() 平面
平面![]() ;
;
(Ⅱ)求三棱锥![]() 体积的最大值;
体积的最大值;
(Ⅲ)若![]() ,点
,点![]() 在线段
在线段![]() 上,求
上,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某赛季甲、乙两位运动员每场比赛得分的茎叶图如图所示.
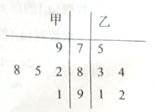
(1)从甲、乙两人的这5次成绩中各随机抽取一个,求甲的成绩比乙的成绩高的概率;
(2)试用统计学中的平均数、方差知识对甲、乙两位运动员的测试成绩进行分析.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱ABCD﹣A1B1C1D1中,底面ABCD为菱形,E为DD1中点.
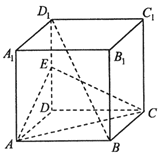
(1)求证:BD1∥平面ACE;
(2)求证:BD1⊥AC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 及点
及点![]() ,
,![]() .
.
(1)若直线![]() 平行于
平行于![]() ,与圆
,与圆![]() 相交于
相交于![]() ,
,![]() 两点,
两点,![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)在圆![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,求点
?若存在,求点![]() 的个数;若不存在,说明理由.
的个数;若不存在,说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱![]() 中,底面
中,底面![]() 是边长为2的正方形,
是边长为2的正方形, ![]() 分别为线段
分别为线段![]() ,
, ![]() 的中点.
的中点.
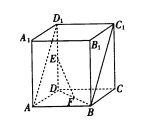
(1)求证: ![]() ||平面
||平面![]() ;
;
(2)四棱柱![]() 的外接球的表面积为
的外接球的表面积为![]() ,求异面直线
,求异面直线![]() 与
与![]() 所成的角的大小.
所成的角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】通过随机询问100名性别不同的大学生是否爱好踢毽子,得到如下的列联表:

随机变量![]() 经计算,统计量K2的观测值k0≈4.762,参照附表,得到的正确结论是( )
经计算,统计量K2的观测值k0≈4.762,参照附表,得到的正确结论是( )
A. 在犯错误的概率不超过5%的前提下,认为“爱好该项运动与性别有关”
B. 在犯错误的概率不超过5%的前提下,认为“爱好该项运动与性别无关”
C. 有97.5%以上的把握认为“爱好该项运动与性别有关”
D. 有97.5%以上的把握认为“爱好该项运动与性别无关”
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com