
【题目】椭圆![]() 离心率为
离心率为![]() ,
,![]() ,
,![]() 是椭圆的左、右焦点,以
是椭圆的左、右焦点,以![]() 为圆心,
为圆心,![]() 为半径的圆和以
为半径的圆和以![]() 为圆心、
为圆心、![]() 为半径的圆的交点在椭圆
为半径的圆的交点在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)设椭圆![]() 的下顶点为
的下顶点为![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 交于两个不同的点
交于两个不同的点![]() ,是否存在实数
,是否存在实数![]() 使得以
使得以![]() 为邻边的平行四边形为菱形?若存在,求出
为邻边的平行四边形为菱形?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案科目:高中数学 来源: 题型:
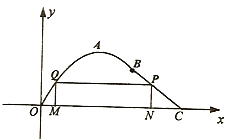
【题目】如图在长为10千米的河流![]() 的一侧有一条观光带,观光带的前一部分为曲线段
的一侧有一条观光带,观光带的前一部分为曲线段![]() ,设曲线段
,设曲线段![]() 为函数
为函数![]() (单位:千米)的图象,且图象的最高点为
(单位:千米)的图象,且图象的最高点为![]() ;观光带的后一部分为线段
;观光带的后一部分为线段![]() .
.
(1)求函数为曲线段![]() 的函数
的函数![]() 的解析式;
的解析式;
(2)若计划在河流![]() 和观光带
和观光带![]() 之间新建一个如图所示的矩形绿化带
之间新建一个如图所示的矩形绿化带![]() ,绿化带仅由线段
,绿化带仅由线段![]() 构成,其中点
构成,其中点![]() 在线段
在线段![]() 上.当
上.当![]() 长为多少时,绿化带的总长度最长?
长为多少时,绿化带的总长度最长?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lg![]() 的图象关于原点对称,其中a为常数.
的图象关于原点对称,其中a为常数.
(Ⅰ)求a的值,并求出f(x)的定义域
(Ⅱ)关于x的方程f(2x)+21g(2x-1)=a在x∈[![]() ,
,![]() ]有实数解,求a的取值范围.
]有实数解,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)求函数![]() 的单调递增区间;
的单调递增区间;
(2)当![]() 时,方程
时,方程![]() 恰有两个不同的实数根,求实数
恰有两个不同的实数根,求实数![]() 的取值范围;
的取值范围;
(3)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位后所得函数
个单位后所得函数![]() 的图象关于原点中心对称,求
的图象关于原点中心对称,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=4sinxcos(x+![]() )+1.
)+1.
(1)求f(![]() )的值;
)的值;
(2)求f(x)的最小正周期;
(3)求f(x)在区间[0,![]() ]上的最大值和最小值.
]上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法错误的是
A. 对分类变量X与Y,随机变量K2的观测值k越大,则判断“X与Y有关系”的把握程度越小
B. 在回归直线方程![]() =0.2x+0.8中,当解释变量x每增加1个单位时,预报变量
=0.2x+0.8中,当解释变量x每增加1个单位时,预报变量![]() 平均增加0.2个单位
平均增加0.2个单位
C. 两个随机变量的线性相关性越强,则相关系数的绝对值就越接近于1
D. 回归直线过样本点的中心(![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A是椭圆E: ![]() =1的左顶点,斜率为k(k>0)的直线交E与A,M两点,点N在E上,MA⊥NA.
=1的左顶点,斜率为k(k>0)的直线交E与A,M两点,点N在E上,MA⊥NA.
(1)当|AM|=|AN|时,求△AMN的面积
(2)当2|AM|=|AN|时,证明: ![]() <k<2.
<k<2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x3+ax2+bx+1的导数![]() 满足
满足![]() ,
,![]() ,其中常数a,b∈R.
,其中常数a,b∈R.
(1)求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)设![]() ,求函数g(x)的极值.
,求函数g(x)的极值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com