
【题目】数列![]() :
: ![]() 满足:
满足: ![]() ,
, ![]() 或1(
或1(![]() ).对任意
).对任意![]() ,都存在
,都存在![]() ,使得
,使得![]() .,其中
.,其中![]()
![]() 且两两不相等.
且两两不相等.
(I)若![]() .写出下列三个数列中所有符合题目条件的数列的序号;
.写出下列三个数列中所有符合题目条件的数列的序号;
①1,1,1,2,2,2;②1,1,1,1,2,2,2,2;③1,l,1,1,1,2,2,2,2
(Ⅱ)记![]() .若
.若![]() ,证明:
,证明: ![]() ;
;
(Ⅲ)若![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(Ⅰ) ②③(Ⅱ)见解析(Ⅲ)![]() 的最小值为
的最小值为![]()
【解析】试题分析:(Ⅰ)依据定义检验给出的数列是否满足要求条件.(Ⅱ)当![]() 时,
时, ![]() 都在数列中出现,可以证明
都在数列中出现,可以证明![]() 至少出现4次,2至少出现2次,这样
至少出现4次,2至少出现2次,这样![]() . (Ⅲ)设
. (Ⅲ)设![]() 出现频数依次为
出现频数依次为![]() .同(Ⅱ)的证明,可得:
.同(Ⅱ)的证明,可得: ![]() ,
, ![]() ,
, ![]() ,┄,
,┄, ![]() ,
, ![]() ,
, ![]() ,则
,则![]() ,我们再构造数列:
,我们再构造数列:
![]() ,证明该数列满足题设条件,从而
,证明该数列满足题设条件,从而![]() 的最小值为
的最小值为![]() .
.
解析:(Ⅰ)对于①,![]() ,对于
,对于![]() ,
, ![]() 或
或![]() ,不满足要求;对于②,若
,不满足要求;对于②,若![]() ,则
,则![]() ,且
,且![]() 彼此相异,若
彼此相异,若![]() ,则
,则![]() ,且
,且![]() 彼此相异,若
彼此相异,若![]() ,则
,则![]() ,且
,且![]() 彼此相异,故②符合题目条件;同理③也符合题目条件,故符合题目条件的数列的序号为②③.
彼此相异,故②符合题目条件;同理③也符合题目条件,故符合题目条件的数列的序号为②③.
注:只得到 ② 或只得到 ③ 给[ 1分],有错解不给分.
(Ⅱ)当![]() 时,设数列
时,设数列![]() 中
中![]() 出现频数依次为
出现频数依次为![]() ,由题意
,由题意![]() .
.
① 假设![]() ,则有
,则有![]() (对任意
(对任意![]() ),与已知矛盾,所以
),与已知矛盾,所以![]() .同理可证:
.同理可证: ![]() .
.
② 假设![]() ,则存在唯一的
,则存在唯一的![]() ,使得
,使得![]() .那么,对
.那么,对![]() ,有
,有![]() (
(![]() 两两不相等),与已知矛盾,所以
两两不相等),与已知矛盾,所以![]() .
.
综上: ![]() ,
, ![]() ,
, ![]() ,所以
,所以![]() .
.
(Ⅲ)设![]() 出现频数依次为
出现频数依次为![]() .同(Ⅱ)的证明,可得:
.同(Ⅱ)的证明,可得: ![]() ,
, ![]() ,
, ![]() ,┄,
,┄, ![]() ,
, ![]() ,
, ![]() ,则
,则![]() .
.
取![]() 得到的数列为:
得到的数列为:
![]()
下面证明![]() 满足题目要求.对
满足题目要求.对![]() ,不妨令
,不妨令![]() ,
,
① 如果![]() 或
或![]() ,由于
,由于![]() ,所以符合条件;
,所以符合条件;
② 如果![]() 或
或![]() ,由于
,由于![]() ,所以也成立;
,所以也成立;
③ 如果![]() ,则可选取
,则可选取![]() ;同样的,如果
;同样的,如果![]() ,
,
则可选取![]() ,使得
,使得![]() ,且
,且![]() 两两不相等;
两两不相等;
④ 如果![]() ,则可选取
,则可选取![]() ,注意到这种情况每个数最多被选取了一次,因此也成立.综上,对任意
,注意到这种情况每个数最多被选取了一次,因此也成立.综上,对任意![]() ,总存在
,总存在![]() ,使得
,使得![]() ,其中
,其中![]() 且两两不相等.因此
且两两不相等.因此![]() 满足题目要求,所以
满足题目要求,所以![]() 的最小值为
的最小值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数![]() ,记
,记![]() .
.
(1)求证: ![]() 在区间
在区间![]() 内有且仅有一个实数;
内有且仅有一个实数;
(2)用![]() 表示
表示![]() 中的最小值,设函数
中的最小值,设函数![]() ,若方程
,若方程![]() 在区间
在区间![]() 内有两个不相等的实根
内有两个不相等的实根![]() ,记
,记![]() 在
在![]() 内的实根为
内的实根为![]() .求证:
.求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() 为常数,设
为常数,设![]() 为自然对数的底数.
为自然对数的底数.
(1)当![]() 时,求
时,求![]() 的最大值;
的最大值;
(2)若![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,求
,求![]() 的值;
的值;
(3)设![]() ,若
,若![]() ,对于任意的两个正实数
,对于任意的两个正实数![]() ,证明:
,证明: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在底面是菱形的四棱锥![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,点
,点![]() 分别为
分别为![]() 的中点,设直线
的中点,设直线![]() 与平面
与平面![]() 交于点
交于点![]() .
.
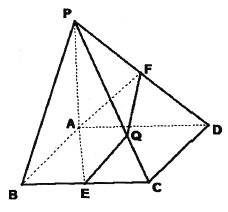
(1)已知平面![]() 平面
平面![]() ,求证:
,求证: ![]() .
.
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足:
满足: ![]() ,
, 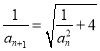 ,
, ![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() ,试确定
,试确定![]() 的值,使得数列
的值,使得数列![]() 为等差数列;
为等差数列;
(3)将数列![]() 中的部分项按原来顺序构成新数列
中的部分项按原来顺序构成新数列![]() ,且
,且![]() ,求证:存在无数个满足条件的无穷等比数列
,求证:存在无数个满足条件的无穷等比数列![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线![]() 的焦点为
的焦点为![]() ,准线为
,准线为![]() ,点
,点![]() 在抛物线
在抛物线![]() 上,已知以点
上,已知以点![]() 为圆心,
为圆心, ![]() 为半径的圆
为半径的圆![]() 交
交![]() 于
于![]() 两点.
两点.
(Ⅰ)若![]() ,
, ![]() 的面积为4,求抛物线
的面积为4,求抛物线![]() 的方程;
的方程;
(Ⅱ)若![]() 三点在同一条直线
三点在同一条直线![]() 上,直线
上,直线![]() 与
与![]() 平行,且
平行,且![]() 与抛物线
与抛物线![]() 只有一个公共点,求直线
只有一个公共点,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com